Übung Kürzeste Wege in Graphen
Aus ProgrammingWiki

Inhaltsverzeichnis |
Unbewertete Graphen
Übung 1.1
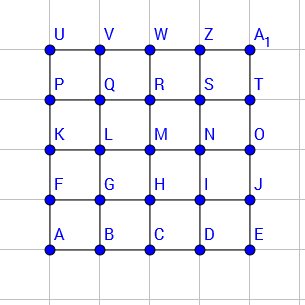
Überlegen Sie, wie viele verschiedene kürzeste Wege es in einem "Manhatten-Graphen" mit neun, sechzehn, fünfundzwanzig oder beliebig vielen Knoten gibt. Finden Sie so viele Wege wie möglich und versuchen sie, eine allgemeine Lösung (eine systematische Aufzählung oder eine allgemeine Formel) zu finden.
Hinweis: Die Anzahl der kürzesten Wege von einem beliebigen Punkt zum Endpunkt ist gleich der Summe der kürzesten Wege von den beiden Knoten, die als erster Schritt in Frage kommen.
Hinweis: Dieses Problem ist auch als "Taxigeometrie" bekannt.
Übung 1.2
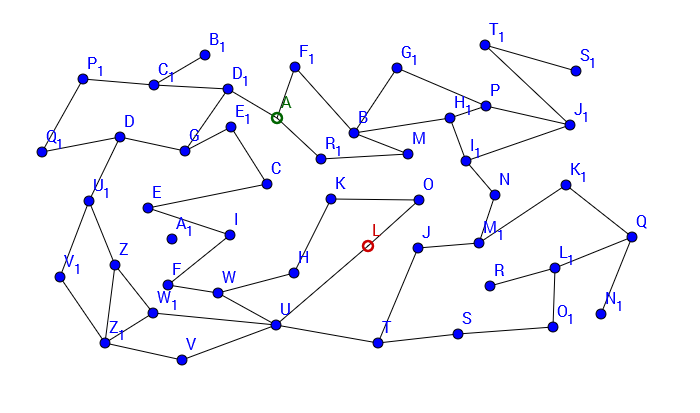
Finden Sie den kürzesten Weg mittels Breitensuche oder mit "Scharfem Hinsehen".
Übung Kürzeste Wege in bewerteten Graphen
Übung 2.1
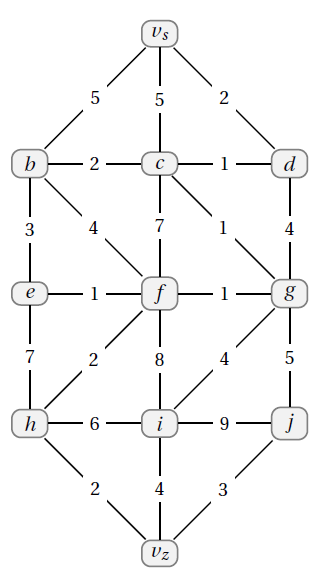
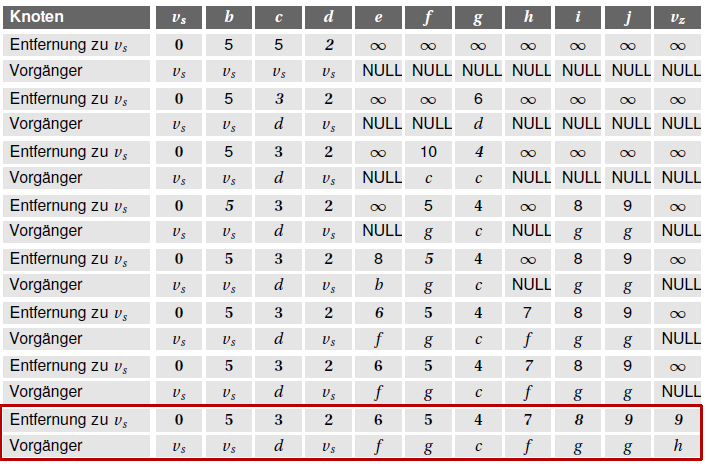
- Führen Sie den Dijkstra-Algorithmus per Hand für folgende Graphendarstellung aus.
- Legen Sie dazu eine Tabelle an.
Übung 2.2
- Implementieren Sie den Floyd-Algorithmus in einer Programmiersprache Ihrer Wahl.
- Lesen Sie dazu eine Matrix ein (alternativ: im Quelltext hardcoden)
- Wenden Sie den Algorithmus an.
- Geben Sie die Ergebnismatrix aus.
- Um ihren Algorithmus zu testen können Sie hier Eingabematrizen und die korrekte Ausgabematrix generieren.
Übung 2.3
Machen Sie sich selbstständig mit verschiedenen Datenstrukturen und ihren Vor-/Nachteilen für die verschiedenen Algorithmen vertraut. (Bsp. Fibonacci-Heap)
Übung 2.4
- Machen Sie sich mit weiteren Algorithmen zur Bestimmung des kürzesten Weges vertraut.
- Welche Charakteristiken und Unterschiede weisen diese auf? (Bsp. A*-Algorithmus, Bellman-Ford-Algorithmus)
Übung 2.5*
- Fügen Sie die folgende Klassen in ihre IDE ein.
- Vervollständigen Sie die Klasse DijkstraAlgorithm mithilfe des in Kommentaren angegebenen Pseudocodes.
- Testen Sie den Algorithmus auf Funktionsfähigkeit mithilfe der folgenden JUnit Test Klasse: