Aus ProgrammingWiki

Sie sollen diese JAVA-Klasse in Netbeans oder Eclipse benutzen. Sie sollen nur richtige Eingaben im Konsole (oben) schreiben :)
Wenn Sie die Fragen haben , probiere ich verschaffen . Viel Erfolg!

Inhaltsverzeichnis 1 Graphen in Java 1.1 Algorithmus von Prim 1.1.1 Java Program to Find MST(Minimum Spanning Tree) using Prim’s Algorithm 1.2 Create a Balanced Binary Tree of the Incoming Data 1.3 Implement Binary Tree 1.3.1 Find Number of Spanning Trees in a Complete Bipartite Graph 2 Aufgaben 2.1 Aufgabe1 3 Übung zu Gozinto-Graphen 4 Übung zu Bipartität

Graphen in Java

Algorithmus von Prim

Der Algorithmus von Prim dient der Berechnung eines minimalen Spannbaumes in einem zusammenhängenden, ungerichteten, kantengewichteten Graphen.
[1]

Java Program to Find MST(Minimum Spanning Tree) using Prim’s Algorithm

import java.util.InputMismatchException; import java.util.Scanner; public class Prims { private final boolean unsettled[]; private final boolean settled[]; private final int numberofvertices; private final int adjacencyMatrix[][]; private final int key[]; public static final int INFINITE = 999; private final int parent[]; public Prims(int numberofvertices) { this.numberofvertices = numberofvertices; unsettled = new boolean[numberofvertices + 1]; settled = new boolean[numberofvertices + 1]; adjacencyMatrix = new int[numberofvertices + 1][numberofvertices + 1]; key = new int[numberofvertices + 1]; parent = new int[numberofvertices + 1]; } public int getUnsettledCount(boolean unsettled[]) { int count = 0; for (int index = 0; index < unsettled.length; index++) { if (unsettled[index]) { count++; } } return count; } public void primsAlgorithm(int adjacencyMatrix[][]) { int evaluationVertex; for (int source = 1; source <= numberofvertices; source++) { for (int destination = 1; destination <= numberofvertices; destination++) { this.adjacencyMatrix[source][destination] = adjacencyMatrix[source][destination]; } } for (int index = 1; index <= numberofvertices; index++) { key[index] = INFINITE; } key[1] = 0; unsettled[1] = true; parent[1] = 1; while (getUnsettledCount(unsettled) != 0) { evaluationVertex = getMimumKeyVertexFromUnsettled(unsettled); unsettled[evaluationVertex] = false; settled[evaluationVertex] = true; evaluateNeighbours(evaluationVertex); } } private int getMimumKeyVertexFromUnsettled(boolean[] unsettled2) { int min = Integer.MAX_VALUE; int node = 0; for (int vertex = 1; vertex <= numberofvertices; vertex++) { if (unsettled[vertex] == true && key[vertex] < min) { node = vertex; min = key[vertex]; } } return node; } public void evaluateNeighbours(int evaluationVertex) { for (int destinationvertex = 1; destinationvertex <= numberofvertices; destinationvertex++) { if (settled[destinationvertex] == false) { if (adjacencyMatrix[evaluationVertex][destinationvertex] != INFINITE) { if (adjacencyMatrix[evaluationVertex][destinationvertex] < key[destinationvertex]) { key[destinationvertex] = adjacencyMatrix[evaluationVertex][destinationvertex]; parent[destinationvertex] = evaluationVertex; } unsettled[destinationvertex] = true; } } } } public void printMST() { System.out.println("SOURCE : DESTINATION = WEIGHT"); for (int vertex = 2; vertex <= numberofvertices; vertex++) { System.out.println(parent[vertex] + "\t:\t" + vertex +"\t=\t"+ adjacencyMatrix[parent[vertex]][vertex]); } } public static void main(String... arg) { int adjacency_matrix[][]; int number_of_vertices; Scanner scan = new Scanner(System.in); try { System.out.println("Enter the number of vertices"); number_of_vertices = scan.nextInt(); adjacency_matrix = new int[number_of_vertices + 1][number_of_vertices + 1]; System.out.println("Enter the Weighted Matrix for the graph"); for (int i = 1; i <= number_of_vertices; i++) { for (int j = 1; j <= number_of_vertices; j++) { adjacency_matrix[i][j] = scan.nextInt(); if (i == j) { adjacency_matrix[i][j] = 0; continue; } if (adjacency_matrix[i][j] == 0) { adjacency_matrix[i][j] = INFINITE; } } } Prims prims = new Prims(number_of_vertices); prims.primsAlgorithm(adjacency_matrix); prims.printMST(); } catch (InputMismatchException inputMismatch) { System.out.println("Wrong Input Format"); } scan.close(); } }

Output --> Lösung

Zusätzliche Informationen

[[https://www.youtube.com/watch?v=Pn874kEc3IA ]] [[2]]

Create a Balanced Binary Tree of the Incoming Data

//This is a java program to insert elements in a Binary Search Tree import java.util.Scanner; class BSTNode { BSTNode left, right; int data; public BSTNode() { left = null; right = null; data = 0; } public BSTNode(int n) { left = null; right = null; data = n; } public void setLeft(BSTNode n) { left = n; } public void setRight(BSTNode n) { right = n; } public BSTNode getLeft() { return left; } public BSTNode getRight() { return right; } public void setData(int d) { data = d; } public int getData() { return data; } } class BSTree { private BSTNode root; public BSTree() { root = null; } public boolean isEmpty() { return root == null; } public void insert(int data) { root = insert(root, data); } private BSTNode insert(BSTNode node, int data) { if (node == null) node = new BSTNode(data); else { if (data <= node.getData()) node.left = insert(node.left, data); else node.right = insert(node.right, data); } return node; } public void inorder() { inorder(root); } private void inorder(BSTNode r) { if (r != null) { inorder(r.getLeft()); System.out.print(r.getData() + " "); inorder(r.getRight()); } } public void preorder() { preorder(root); } private void preorder(BSTNode r) { if (r != null) { System.out.print(r.getData() + " "); preorder(r.getLeft()); preorder(r.getRight()); } } public void postorder() { postorder(root); } private void postorder(BSTNode r) { if (r != null) { postorder(r.getLeft()); postorder(r.getRight()); System.out.print(r.getData() + " "); } } } public class Insertion_BST { public static void main(String[] args) { Scanner scan = new Scanner(System.in); BSTree bst = new BSTree(); System.out.println("Binary Search Tree Insertion Test\n"); int N = 10; for (int i = 0; i < N; i++) { bst.insert(scan.nextInt()); System.out.print("\nPost order : "); bst.postorder(); System.out.print("\nPre order : "); bst.preorder(); System.out.print("\nIn order : "); bst.inorder(); } scan.close(); } }

2. MOEGLICHKEIT

//This is a java program to make a self balancing binary tree for the input data import java.util.Scanner; class SBBSTNodes { SBBSTNodes left, right; int data; int height; public SBBSTNodes() { left = null; right = null; data = 0; height = 0; } public SBBSTNodes(int n) { left = null; right = null; data = n; height = 0; } } class SelfBalancingBinarySearchTrees { private SBBSTNodes root; public SelfBalancingBinarySearchTrees() { root = null; } public boolean isEmpty() { return root == null; } public void clear() { root = null; } public void insert(int data) { root = insert(data, root); } private int height(SBBSTNodes t) { return t == null ? -1 : t.height; } private int max(int lhs, int rhs) { return lhs > rhs ? lhs : rhs; } private SBBSTNodes insert(int x, SBBSTNodes t) { if (t == null) t = new SBBSTNodes(x); else if (x < t.data) { t.left = insert(x, t.left); if (height(t.left) - height(t.right) == 2) if (x < t.left.data) t = rotateWithLeftChild(t); else t = doubleWithLeftChild(t); } else if (x > t.data) { t.right = insert(x, t.right); if (height(t.right) - height(t.left) == 2) if (x > t.right.data) t = rotateWithRightChild(t); else t = doubleWithRightChild(t); } else ; t.height = max(height(t.left), height(t.right)) + 1; return t; } private SBBSTNodes rotateWithLeftChild(SBBSTNodes k2) { SBBSTNodes k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = max(height(k2.left), height(k2.right)) + 1; k1.height = max(height(k1.left), k2.height) + 1; return k1; } private SBBSTNodes rotateWithRightChild(SBBSTNodes k1) { SBBSTNodes k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = max(height(k1.left), height(k1.right)) + 1; k2.height = max(height(k2.right), k1.height) + 1; return k2; } private SBBSTNodes doubleWithLeftChild(SBBSTNodes k3) { k3.left = rotateWithRightChild(k3.left); return rotateWithLeftChild(k3); } private SBBSTNodes doubleWithRightChild(SBBSTNodes k1) { k1.right = rotateWithLeftChild(k1.right); return rotateWithRightChild(k1); } public int countNodes() { return countNodes(root); } private int countNodes(SBBSTNodes r) { if (r == null) return 0; else { int l = 1; l += countNodes(r.left); l += countNodes(r.right); return l; } } public boolean search(int val) { return search(root, val); } private boolean search(SBBSTNodes r, int val) { boolean found = false; while ((r != null) && !found) { int rval = r.data; if (val < rval) r = r.left; else if (val > rval) r = r.right; else { found = true; break; } found = search(r, val); } return found; } public void inorder() { inorder(root); } private void inorder(SBBSTNodes r) { if (r != null) { inorder(r.left); System.out.print(r.data + " "); inorder(r.right); } } public void preorder() { preorder(root); } private void preorder(SBBSTNodes r) { if (r != null) { System.out.print(r.data + " "); preorder(r.left); preorder(r.right); } } public void postorder() { postorder(root); } private void postorder(SBBSTNodes r) { if (r != null) { postorder(r.left); postorder(r.right); System.out.print(r.data + " "); } } } public class Balanced_B_Tree { public static void main(String[] args) { Scanner scan = new Scanner(System.in); SelfBalancingBinarySearchTrees sbbst = new SelfBalancingBinarySearchTrees(); System.out.println("Self Balancing Tree\n"); int N = 10; for (int i = 0; i < N; i++) sbbst.insert(scan.nextInt()); System.out.println("\nPre-order :"); sbbst.preorder(); System.out.println("\nIn-order :"); sbbst.inorder(); System.out.println("\nPost-order :"); sbbst.postorder(); scan.close(); } }

Output --> Loesung

Implement Binary Tree

/* * Java Program to Implement Binary Tree */ import java.util.Scanner; /* Class BTNode */ class BTNode { BTNode left, right; int data; /* Constructor */ public BTNode() { left = null; right = null; data = 0; } /* Constructor */ public BTNode(int n) { left = null; right = null; data = n; } /* Function to set left node */ public void setLeft(BTNode n) { left = n; } /* Function to set right node */ public void setRight(BTNode n) { right = n; } /* Function to get left node */ public BTNode getLeft() { return left; } /* Function to get right node */ public BTNode getRight() { return right; } /* Function to set data to node */ public void setData(int d) { data = d; } /* Function to get data from node */ public int getData() { return data; } } /* Class BT */ class BT { private BTNode root; /* Constructor */ public BT() { root = null; } /* Function to check if tree is empty */ public boolean isEmpty() { return root == null; } /* Functions to insert data */ public void insert(int data) { root = insert(root, data); } /* Function to insert data recursively */ private BTNode insert(BTNode node, int data) { if (node == null) node = new BTNode(data); else { if (node.getRight() == null) node.right = insert(node.right, data); else node.left = insert(node.left, data); } return node; } /* Function to count number of nodes */ public int countNodes() { return countNodes(root); } /* Function to count number of nodes recursively */ private int countNodes(BTNode r) { if (r == null) return 0; else { int l = 1; l += countNodes(r.getLeft()); l += countNodes(r.getRight()); return l; } } /* Function to search for an element */ public boolean search(int val) { return search(root, val); } /* Function to search for an element recursively */ private boolean search(BTNode r, int val) { if (r.getData() == val) return true; if (r.getLeft() != null) if (search(r.getLeft(), val)) return true; if (r.getRight() != null) if (search(r.getRight(), val)) return true; return false; } /* Function for inorder traversal */ public void inorder() { inorder(root); } private void inorder(BTNode r) { if (r != null) { inorder(r.getLeft()); System.out.print(r.getData() +" "); inorder(r.getRight()); } } /* Function for preorder traversal */ public void preorder() { preorder(root); } private void preorder(BTNode r) { if (r != null) { System.out.print(r.getData() +" "); preorder(r.getLeft()); preorder(r.getRight()); } } /* Function for postorder traversal */ public void postorder() { postorder(root); } private void postorder(BTNode r) { if (r != null) { postorder(r.getLeft()); postorder(r.getRight()); System.out.print(r.getData() +" "); } } } /* Class BinaryTree */ public class BinaryTree { public static void main(String[] args) { Scanner scan = new Scanner(System.in); /* Creating object of BT */ BT bt = new BT(); /* Perform tree operations */ System.out.println("Binary Tree Test\n"); char ch; do { System.out.println("\nBinary Tree Operations\n"); System.out.println("1. insert "); System.out.println("2. search"); System.out.println("3. count nodes"); System.out.println("4. check empty"); int choice = scan.nextInt(); switch (choice) { case 1 : System.out.println("Enter integer element to insert"); bt.insert( scan.nextInt() ); break; case 2 : System.out.println("Enter integer element to search"); System.out.println("Search result : "+ bt.search( scan.nextInt() )); break; case 3 : System.out.println("Nodes = "+ bt.countNodes()); break; case 4 : System.out.println("Empty status = "+ bt.isEmpty()); break; default : System.out.println("Wrong Entry \n "); break; } /* Display tree */ System.out.print("\nPost order : "); bt.postorder(); System.out.print("\nPre order : "); bt.preorder(); System.out.print("\nIn order : "); bt.inorder(); System.out.println("\n\nDo you want to continue (Type y or n) \n"); ch = scan.next().charAt(0); } while (ch == 'Y'|| ch == 'y'); } }

Output --> Loesungen

Find Number of Spanning Trees in a Complete Bipartite Graph

1. Import Scanner
2. Implementieren Sie eine Klasse NumOfSpanningBipartite,die folgende Anforderungen erfuellt:

- Die integer Zahlen "firstSetSize" und "secondSetSize" werden werden im Methode als Parameter erwartet und in privaten Attributen abgespeichert.
- return (this.firstSetSize^(this.secondSetSize - 1)) *(this.secondSetSize ^ (this.firstSetSize -1));
3. Implementieren Sie eine main- Klasse nur mit String[args] Parameter
- Deklarieren Sie m und n als Zahlvariable(int)
- Benutzen Sie die Scanner Prozedure.
- Drucken Sie " Enter the size of the bipartite graph(m and n)
- Benutzen Sie eine Methode Scanner fuer m und n (next...())
- Erzeugen Sie ein neues Objekt bipartite.
- Benutzen Sie System.out.println(...+bipartite.numerOfSpanningTree(m,n)))
- Schliessen Sie Scanner Methode.

OUTPUT:

Ich hoffe, dass ganze Gruppe damit zurechtkommen :D Aber machen Sie keine Sorgen, die Loesungen werde ich nach der Unterrichte schreiben.Wenn jemand eine Frage habt, probiere ich zu helfen! :}

Aufgaben

Aufgabe1

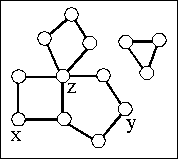
Wieviele Zusammenhangskomponenten hat der Graph?

Ist der Graph bipartit?

dG(x,y) =?

dG(x,z)

Wieviel Kreise gibt es im Graphen ?

Wieviele Wege gibt es von x nach y?

Übung zu Gozinto-Graphen

Zur Produktion eines Endproduktes A werden 4 Teile vom Typ B, 2 Teile Typ C, 3Teile Typ D und 1Teil vom Typ E benötigt. Typ E fließt mit je 1Teil auch noch in die Produktion von D und C ein. Ein weiterer Bautyp F fließt zu je 2Stk in die Produktion von C und mit je 1Stk in die Produktion von B ein.
1.Zeichne einen Gozinto-Graphen zu dem beschriebenen Sachverhalt.
2.Wir erhalten einen Auftrag und sollen 150A, 400B, 50C, 100D, 200E und 300F bereitstellen. Ermitteln sie den Gesamtbedarf für alle Teile der Produktionskette!

LÖSUNG

Direktmatrix ------ und ------ Einheitsmatrix

0| 1| 0| 2| 0| 0      |      1| 0| 0| 0| 0| 0
0| 0| 0| 0| 0| 4      |      0| 1| 0| 0| 0| 0
0| 0| 0| 1| 1| 1      |      0| 0| 1| 0| 0| 0
0| 0| 0| 0| 0| 2      |      0| 0| 0| 1| 0| 0
0| 0| 0| 0| 0| 3      |      0| 0| 0| 0| 1| 0
0| 0| 0| 0| 0| 0      |      0| 0| 0| 0| 0| 1

Einheitsmatrix - Direktmatrix

1|-1| 0| 2| 0| 0
0| 1| 0| 0| 0|-4  +4*Zeile6
0| 0| 1|-1|-1|-1  +Zeile6
0| 0| 0| 1| 0|-2  +2*Zeile6
0| 0| 0| 0| 1|-3  +3*Zeile6
0| 0| 0| 0| 0| 1

1|-1| 0| 2| 0| 0  +2*Zeile4 | +Zeile2
0| 1| 0| 0| 0| 4
0| 0| 1|-1|-1| 1
0| 0| 0| 1| 0| 2  +Zeile5 |+Zeile4
0| 0| 0| 0| 1| 3
0| 0| 0| 0| 0| 1

Ergebnis der Invertierung

1| 1| 0| 2| 0| 8    
0| 1| 0| 0| 0| 4
0| 0| 1| 1| 1| 6   
0| 0| 0| 1| 0| 2  
0| 0| 0| 0| 1| 3
0| 0| 0| 0| 0| 1

Multiplikation mit Primärbedarfvektor

(1*300)+(1*400)+(0*200)+(2*50)+(0*100)+(8*150) = 2000
0+400+0+0+0+600 = 1000
0+0+200+50+100+900 = 1250
0+0+0+50+0+300 = 350
0+0+0+0+100+450 = 550
0+0+0+0+0+150 = 150

Übung zu Bipartität

• Aufgabe: Erstelle ein Programm welches testet ob ein zusammenhängender Graph bipartit ist oder nicht. Orientiere dich dabei an dem in der Vorlesung vorgestellten Algorithmus im Abschnitt: Konstruktion einer Zerlegung von V in S und T!
  
• Zusatzaufgabe: Schreibe das Programm so um, dass es auch für nicht zusammenhängende Graphen funktioniert.
• Zusatzaufgabe: Führe eine empirische Effizienzanalyse mit dem Testprogramm durch.
  

Hilfestellung zur Aufgabenstellung findest du in dem folgenden Code für ein funktionierendes Testprogramm, welches allerdings noch einige Optimierungsmöglichkeiten bietet!

• Zusatzaufgabe: Hat das vorgestellte Programm linearen Aufwand? Begründe deine Antwort!

//Javaprogram zum testen ob ein Graph bipartit ist oder nicht import java.util.*; import java.lang.*; import java.io.*; //=================================================================================================================================== class Bipartite { final static int KnotenAnzahl = 4; // Anzahl der Knoten boolean istBipartit(int G[][],int start) // Testunktion für einen Graphen G[][]. Startknoten muss mit übergeben werden. { //True wenn bipartit, false wenn nicht. // Wert 1 steht für Farbe a, 0 für Farbe b int FarbenArray[] = new int[KnotenAnzahl]; // Farbenarray - Zuordnung von Farben zu jedem Knoten. for (int i=0; i<KnotenAnzahl; ++i) FarbenArray[i] = -1; // Solange noch keine Farbe zugeordnet wurde hat jeder Knoten den Wert '-1' FarbenArray[start] = 1; // Startknoten färben LinkedList<Integer>keller = new LinkedList<Integer>(); // Keller für neu eingefärbte Knoten keller.add(start); while (keller.size() != 0) { // Knoten aus dem Keller holen und in u speichern int u = keller.poll(); for (int v=0; v<KnotenAnzahl; ++v) { if (G[u][v]==1 && FarbenArray[v]==-1) //wenn Graph von u nach v existiert und v noch keine Farbe hat... { FarbenArray[v] = 1-FarbenArray[u]; //färbung zu 0 wenn u 1 ist, wenn u 0 ist färbung zu 1 keller.add(v); //neu gefärbten Knoten zur weiteren untersuchung in den Keller legen } else if (G[u][v]==1 && FarbenArray[v]==FarbenArray[u]) //wenn Graph von u nach v existiert und beide // Knoten die selbe farbe haben... return false; } } return true; } //=================MAIN================= public static void main (String[] args) { //Graph als Adjazenzmatrix erstellen int G[][] = {{0, 1, 1, 1}, {1, 0, 1, 0}, {1, 1, 0, 1}, {1, 0, 1, 0}}; //Testfunktion aufrufen Bipartite b = new Bipartite(); if (b.istBipartit(G, 0)) System.out.println("Graph ist bipartit"); else System.out.println("Graph ist nicht bipartit"); } }