Euler-Kreise und -Wege

Aus ProgrammingWiki

Wechseln zu: Navigation, Suche

Patrick Schmidt und Kevin Richter

Inhaltsverzeichnis

Einführung

Leonhard Euler

  • geboren am 15. April 1707 in Basel
  • gestorben am 18. September 1783 in Sankt Petersburg
  • war einer der bedeutendsten Mathematiker und Physiker
  • befasste sich mit vielen Themen der Analysis, Zahlentheorie
  • löste das Königsberger Brückenproblem
  • Mitbegründer der Graphentheorie

Motivation

  • Im Bereich der eulerschen Graphen beschäftigt man sich im Vergleich zu anderen Gebieten der Graphentheorie mit ganzen Rundreise durch Graphen.
  • Dies ist ein völlig neuer Ansatz und enthält ebenso neue Problemtypen.


Euler-Graphen

Definition

Was sind Euler-Graphen?

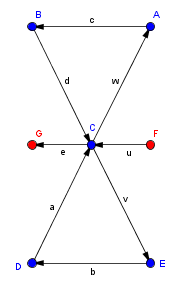
  • $G=(V,E)$ ist genau dann eulersch, wenn ein Weg bzw. Kreis $P$ existiert, für den gilt $G(|E|)=P(|E|)$
  • Das bedeutet eulersche Graphen sind Graphen bei denen alle Kanten genau einmal durchlaufen werden müssen.


Ist folgender Graph eulersch? Eulergraph.PNG


Euler Kreise

  • Ein Eulerkreis oder auch geschlossener Eulerzug bzw. Eulertour ist ein Zyklus in einem Graphen, der alle Kanten des Graphen enthält.
  • Desweiteren haben sie einen gemeinsamen Start bzw. Endpunkt.
  • enthält ein Graph einen Eulerkreis, so wird dieser als eulersch bezeichnet.
  • Das Problem das sich mit dem Auffinden dieser beschäftigt heißt Eulerkreisproblem.

Kerich VL bsp eulerkreis2.png Kerich Gerichteter graph vorlesung Eulerkreis.png Kerich VL bsp eulerkreis.png


Euler Wege

  • Ein Eulerweg oder auch offener Eulerzug ist in der Graphentheorie die Bezeichnung für eine Kantenfolge eines Graphen, bei der jede Kante genau einmal durchlaufen wird.
  • Dabei sind der Start- und Endknoten nicht identisch.
  • Insofern ein Graph nur einen Eulerweg besitzt, bezeichnet man ihn als semi-eulersch.

Euleweg 1.png Eulerweg 2.png


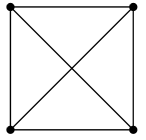
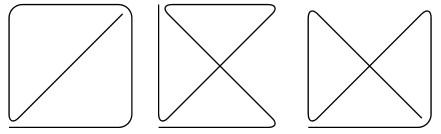
Das Haus des Nikolaus

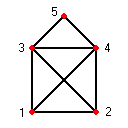
Ein altes, aber heute noch präsentes Kinderrätsel: "Das-ist-das-Haus-des-Ni-ko-laus"

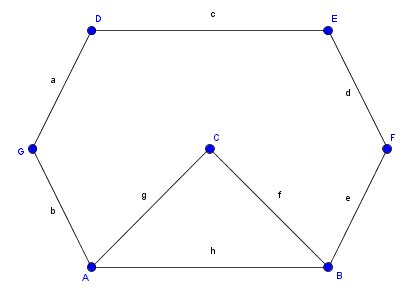
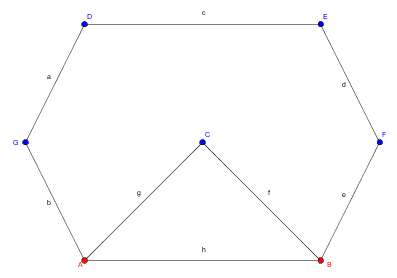
  • Gegeben sei ein Graph $G(V,E)$ mit $V$=5 und $E$=8:

Nikolaus haus.gif Nikolaus haus.png

  • Ziel hierbei ist es, alle Kanten des Graphen miteinander zu verbinden ohne Abzusetzen.
  • Versuchen Sie es: Zeichen Sie diesen Graphen nach der vorgegebenen Zielstellung. Was fällt ihnen auf?



Algorithmen

Algorithmus von Fleury

  • Beim Algorithmus von Fleury sind Brückenkanten von besonderer Bedeutung.
  • Dies sind Kanten, ohne die der Graph in zwei Komponenten zerfallen würde.
  • Input: Graph $G(V,E)$
  • Output: Eulerkreis oder Eulerweg
1. Wähle einen beliebigen Knoten $v \in V$ als aktuellen Knoten.
2. Wähle nun unter den mit dem aktuellen Knoten $v$ inzidenten Kanten eine beliebige Kante $e \in E$ aus.
   Dabei ist $e$ so zu wählen, dass diese im unmarkierten Graphen keine Brückenkante ist.
3. Markiere $e$ und entferne sie.
4. Wähle den anderen Knoten $w \in V$ von $e$ als neuen aktuellen Knoten.
5. Wenn noch unmarkierte Kanten existieren, dann gehe zu Schritt 2.
  • Mit einer Laufzeit von $O(|E|)$ kann festgestellt werden, ob eine Kante eine Brückenkante ist.
  • Für das Entfernen der Kanten werden $|E|$ Iterationen benötigt.
  • Somit ergibt sich eine Gesamtlaufzeit von $O(|E$2$|)$.

Algorithmus von Hierholzer

  • Dieser Algorithmus macht sich die Eigenschaften zu nutze, dass eulersche Graphen in paarweise Kantendisjunkte Kreise zerlegt werden können.
  • Der Algorithmus funktioniert demnach wie folgt:


  • Man wählt einen beliebigen Knoten aus dem Graphen und bildet über eine Folge von Kanten einen Kreis.
  • Danach wählt man einen Knoten aus den bereits gebildeten Kreis/en von dem aus es noch unbesuchte Kanten gibt und bildet von diesem Knoten ausgehend erneut einen Zyklus.
    • Ist der Graph semi-eulersch, enthält der Graph zudem zusätzlich einen Weg zwischen den beiden Knoten mit ungeraden Grad.
  • Dies wiederholt man solange bis der Graph mithilfe der Subkreise zu einem Eulerkreis oder ergänzt um einen Weg zu einen Eulerweg zusammengesetzt werden kann.


  • Input: Graph $G(V,E)$
  • Output: Eulerkreis oder Eulerweg 
1. setze $C: = 0 $; wähle $ v \in V$ beliebig.
2. wähle weitere Knoten $v$i $\in V$, sodass $(v,...,v$i) ein Weg in $G$ ist, und zwar so lange bis ein Kreis $C'$ entsteht.  Füge $C'$ bei $v$ an $C$ an.
3. Falls $C$ ein Eulerkreis ist $STOPP$ und Ausgabe von $C$.
4. Ansonsten wähle einen in $C$ enthaltenen Knoten $w \in V$, der zu einer nicht in $C$ enthaltenen Kante gehört und gehe zum 2.Schritt
  • Er ist wesentlich effizienter, da er ein Eulerkreis oder Eulerweg in linearzeit,d.h mit einer Laufzeit von $O(|E|)$ auffinden kann.
  • Das liegt daran, dass der Algorithmus nur die Kanten entlang geht und Zyklen bildet.
  • Damit ist der Aufwand von der Kantenzahl des Graphen abhängig.

https://www-m9.ma.tum.de/graph-algorithms/hierholzer/index_de.html

Das Postbotenproblem

Definition

  • Benannt nach dem chinesischen Mathematiker Mei-Ko Kwan der sich ersmals 1962 damit beschäftigte.
  • Ein Postbote soll die Briefe (auf beiden Seiten der Straße gleichzeitig) in einem Straßennetzwerk (Stadt) zustellen und anschließend zum Postamt zurückkehren.
  • Dies soll in kürzester Zeit geschehen.

Modellierung

  • Das Problem kann mithilfe eines Graphen dargestellt werden, wobei die Kreuzungen als Knoten, die Straßen als Kanten, sowie deren Länge(Zeit) als Gewicht betrachtet werden.
  • Um alle Straßen in kürzester Zeit überqueren und wieder beim Ausgangspunkt landen zu können, muss nach einem möglichst kurzen Eulerkreis gesucht werden.

Lösung

  • Existieren keine Knoten mit ungeraden Grad ist die Lösung der jeweilige Eulerkreis.

Problem:

  • Was tun wen der Graph nicht eulersch ist?

Vorüberlegung:

  • ein Graph $G(V,E)$ ist genau dann nicht eulersch, wenn $d$$G$$(v)$ ungerade für mindestens ein Knoten ist.
  • Die Anzahl der Knoten mit ungeraden Grad in Graphen ist immer gerade.

Lösung:

  • es müssen Kanten zwischen diesen Knoten hinzugefügt werden, sodass der Graph wieder eulersch wird.
  • Das bedeutet für den Postman einfach ein doppeltes Ablaufen der Straße.



Algorithmus

Für ungerichtete Graphen gilt:

1. Fasse die Knoten ungeraden Grades zu einer Teilmenge $V'$ von $V$ zusammen und definiere $G'$ als den vollständigen Graphen auf den Knoten $V'$
2. Definiere eine Bewertung auf $G'$ mithilfe kürzester Wege (z.B. Algorithmus von Dijkstra)
3. Bestimme ein bezüglich dieser Bewertung minimales Matching $M$ auf $G'$ und füge zu $G$ die Kanten des Matchings hinzu
4. Bestimme den Eulerkreis von $G$ (z.B. Algoritmus von Hierholzer)


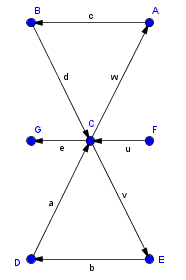
Für gerichtete Graphen gilt:

1. Fasse die Knoten von $V$ mit $d$$-$$G$$(v)$ $\lt$ $d$$+$$G$$(v)$ zu einer Menge $V$$+$ und die Knoten von $V$ mit $d$$-$$G$$(v)$ $\gt$ $d$$+$$G$$(v)$ zu einer Menge $V$$-$ zusammen.
2. Definiere $G'$ als den vollständigen bipartiten gerichteten Graphen zwischen $V$$-$ und $V$$+$.
3. Definiere auf diesem Hilfsgraphen eine Bewertung mithilfe kürzester Wege.
4. Wähle eine bezüglich dieser Bewertung minimale Teilmenge von Pfeilen aus dem Hilfsgraphen aus und füge sie zu $G$ hinzu
5. Bestimme den Eulerkreis von $G$


Anwendungsgebiete

Königsberger Brückenproblem

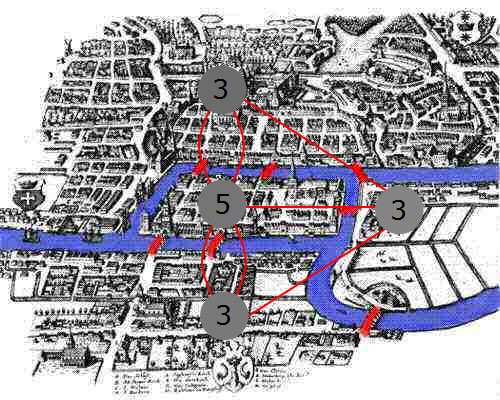
  • Das Problem bestand darin, zu klären, ob es einen Weg gibt, bei dem man alle sieben Brücken genau einmal überquert, und wenn ja, ob auch ein Rundweg möglich ist, bei dem man wieder zum Ausgangspunkt gelangt.

Brückenproblem.png nach Postbotenproblematik Brückenproblem pb.png

  • Laut Eulers Definition des Euler-Graphen kann dieser Graph nicht eulersch sein.
  • Bei näheren Hinschauen fällt auf, dass er auch nicht semi-eulersch ist, da die Anzahl der ungeraden Knoten auf 2 limitiert sein muss.
  • Somit hat Euler das Brückenproblem dahinggehend gelöst, dass er bewiesen hat, dass es kein Eulergraph zu diesem Problem gibt.
  • Daraus folgt, dass es in diesem Zusammenhang nicht möglich ist alle Brücken einmalig zu überqueren.


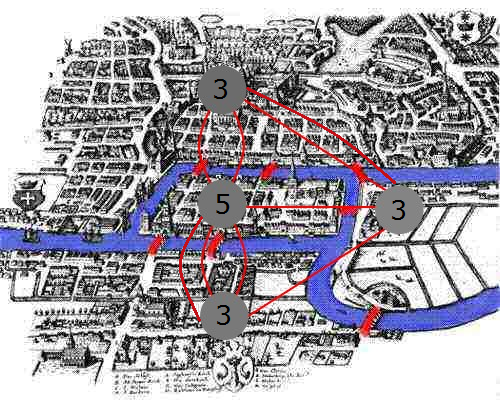
  • Das Postbotenproblem liefert hier aber eine Lösung bei der man zumindest alle Brücken überqueren kann und zum Anfangspunkt zurückehrt.
  • Jedoch ist dies in Hinblick auf die ursrprüngliche Fragestellung nur ein Trost, da nur zwei der drei Bedingungen erfüllt wurden.

Weitere Gebiete

  • weitere Anwendungsgebiete in der Praxis sind besonders in Bezug auf das Postbotenproblem schnell gefunden
  • Im Großen und Ganzen überall da wo es darum geht alle Wege zwischen Punkten zu passieren und gegebenenfalls wieder an der Startposition zu landen
  • Beispiele hierfür sind:
  • Postzusteller, wie bereits geklärt
  • Müllabfuhr
  • Museentouren
  • im Tourismus
  • Zustellungsservices
  • Zulieferer
  • persönliche Einkäufe

Quellen

Von „https://programmingwiki.de/Euler-Kreise_und_-Wege“
Persönliche Werkzeuge