Teile und Herrsche 1 SS11
Aus ProgrammingWiki

Inhaltsverzeichnis |
Die Idee
Teile und Herrsche
Bei der systematischen Programmentwicklung und für die unmittelbare Ableitung von Aufwandsaussagen sind verschiedene Entwurfsmethoden für Algorithmen hilfreich. Zu den Entwurfsmethoden gehören zum Beispiel:
- Teile und Herrsche
- Greedy-Algorithmen
- dynamisches Programmieren
Teile und Herrsche (engl. "divide and conquer", lat. "divide et impera") ist die Entwurfsmethode für Algorithmen die wir nachfolgend genauer betrachten wollen.
Diese Methode hat seinen Ursprung als Redewendung und Strategie in der Kriegsführung. Bereits um 500 v. Chr. erwähnte Sunzi, ein chinesischer General, sinngemäß "Teile und Herrsche" als Strategie der chinesischen Kriegskunst. Mit divise pour régner (frz. für "teilen, um zu herrschen") wurde sie als Ausspruch des frz. Königs Ludwig XI. (*1423 †1483) bekannt. Des Weiteren ist die Strategie in der römischen Außenpolitik zu Zeiten Julius Caesars wieder zu erkennen. In Bezug auf Kriegsführung besteht die Taktik darin, die Gegner durch gezieltes gegeneinander Ausspielen in kleine Gruppen zu spalten und somit leichter besiegen zu können.
Das Prinzip ist in der Informatik das Gleiche, wenn auch weniger grausam. Die Methode löst Probleme, indem es
- in Teilprobleme zerlegt wird ("divide")
- die Teilprobleme gelöst und
- die Lösungen der Teilprobleme wieder zusammengesetzt werden ("conquer").
Effizienzbetrachtung von Teile und Herrsche
Wir wollen feststellen, ob mit Algorithmen, die nach der Methode "divide and conquer" entworfen wurden, eine Effizienzverbesserung erzielt werden kann. Wir betrachten einen Algorithmus , der unser Problem in
, d.h mit
löst. Der Algorithmus
bearbeitet drei Probleme der Größe
mittels der Prozedur
. Der Gesamtaufwand von unserem Algorithmus
fasst die Teillösungen mit einem Aufwand
zusammen.
Das Ergebnis zeigt, dass eine Effizienzverbesserung von 25 % festgestellt werden kann. Der Aufwand ist jedoch nach wie vor quadratisch, wie der Exponent der Funktion zeigt. Das bedeutet, dass für größere keine große Verbesserung in der Effizienz erzielt werden kann.
Die Betrachtung eines Algorithmus
, der die drei Teilprobleme mit Rekursion löst, verdeutlicht, dass wir uns mit diesem Ergebnis nicht zufrieden geben müssen. Der Basisfall
wird weiterhin vom Algorithmus
übernommen. Es entstehen folgende Aufwandsbeziehungen:
Diese Rekursionsgleichung lösen wir mit dem 1. Fall der Meistermethode.
Die Lösung zeigt, dass durch eine rekursive Lösung die Effizienz dem quadratischen Aufwand gegenüber deutlich verbessert werden kann. Dies veranschaulicht, dass Teile-und-Herrsche-Verfahren immer rekursive Lösungen der gebildeten Teilprobleme enthalten müssen. Die Teilprobleme haben eine geringere Problemgröße bei gleicher Problematik, als das zu lösende Ausgangsproblem. Zur rekursiven Lösung gehört ein allgemeiner Fall wie auch ein Basisfall. Je nach Problem kann es aber auch mehrere Basisfälle geben.
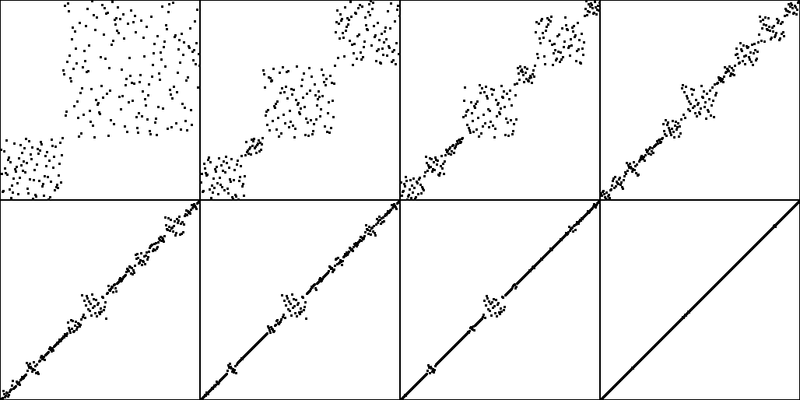
Quicksort
Verfahren
Quicksort (schnelles Sortieren) wurde 1962 von dem britischen Informatiker Charles Anthony Richard Hoare (* 11. Januar 1934) entwickelt.
Die Idee des Algorithmus besteht darin, die Gesamtliste in eine linke und eine rechte Teilliste zu zerlegen, so dass alle Elemente von
kleiner und von
größer sind als das Vergleichsobjekt
.
Wir vereinbaren, dass die Elemente von paarweise verschieden sind, also für alle
gilt
. Diese Einschränkung ist nicht notwendig, aber sinnvoll, da es sich um Schlüssel zur Identifikation von Datensätzen handelt. Wir verabreden des Weiteren, dass es sich um natürliche Zahlen handelt.
Zusätzlich legen wir fest, dass wir das am weitesten links stehende Element aus
als Vergleichselement
verwenden, also
. Die Listen
,
und
bilden die sortierte Gesamtliste
genau in dieser genannten Reihenfolge. Aus Effizienzgründen werden die Teillisten mit Quicksort sortiert.
Es gibt zwei Basisfälle: ist leer oder besteht aus nur einem Element, dann ist
. Wenn man
in die Teillisten
und
zerlegt, entstehen durch die Entnahme von
Listen, die mindestens ein Element weniger enthalten als
. Somit wird nach endlich vielen Zerlegungen einer der Elementarfälle erreicht.
Funktionsorientierte Beschreibung
traditionelles Quicksort
Bestimmen des Vergleichselements, das erste Element der ungeordneten Liste
Erzeugen der linken Teilliste
Erzeugen der rechten Teilliste
Prozedur in der die linke und rechte Teilliste zusammengefügt werden. Die linke und rechte Liste werden sortiert und dann anschließend zusammengefügt. Das geschieht in der Form linke Liste, Vergleichselement, rechte Liste.
Im Gegensatz zum traditionellen Quicksort arbeitet Quicksort in einem sog. Multiple-value-context. Das heißt Funktionen können beliebig (aber endlich) viele Funktionswerte besitzen, die dann an die entsprechenden Funktionen weitergegeben werden können und von diesen weiterverarbeitet werden.
Multiple-Value-Quicksort
Effizienzbetrachtung von Quicksort
Best Case
Am Besten arbeitet Quicksort, wenn die Teillisten ungefähr gleich groß sind. Es ergibt sich die Lösung von
einem Aufwand . Zur Lösung der Rekursionsgleichung haben wir die Meistermethode verwendet. Die in der allgemeinen Form
vorkommenden Variablen enthalten für Teile- und Herrsche-Verfahren besondere Bedeutung. Die Variable steht für die Anzahl der Teilprobleme und
für die Größe eines Teilproblems, wobei die Zerlegung immer aufgehen sollte.
Worst Case
Den Worst Case des Verfahrens kennzeichnet eine vollständig sortierte Liste.
Eigentlich wäre der Sortieraufwand somit gleich null, da das Ergebnis bereits vorliegt.
Die Rekursionsgleichung für
Mit der Iterationsmethode kann die Gleichung leicht gelöst werden.
Das in die Summenschreibweise übertragen
Average Case
Gehen wir davon aus, dass jede der Teillistenlängen mit der gleichen Wahrscheinlichkeit von
auftritt, dann sprechen wir von dem Average Case.
Dann gilt
Setzt man dies ein, so ergibt das
Jetzt wollen wir das Summenzeichen beseitigen, indem wir die Differenz bilden
Mit den Harmonischen Zahlen und deren bekannten Schranken
ergibt sich dann
Interne Suchverfahren
darauf wird an dieser Stelle nicht eingegangen.
Mergesort
Verfahren
Quicksort und Mergesort sind eng verwandt. Merge bedeutet soviel wie "zusammenführen" oder "einfädeln", ähnlich wie es im Straßenverkehr geschieht, wenn zwei Fahrspuren zusammengeführt werden. Die Übersetzung "Sortieren durch Mischen" trifft nicht zu. Die zu sortierende Gesamtliste
wird zunächst mit in zwei etwa gleich große Teillisten geteilt.
Es erfolgen im Gegensatz zu Quicksort also keine Vorsortierungen oder Vergleiche. steht für die ganzzahlige Division, sodass entweder
oder
gilt.
Im Conquer-Schritt sollen
und
rekursiv durch Mergesort sortiert werden. Es gelten die gleichen Elementarfälle wie bei Quicksort. Die dadurch entstandenen sortierten Teillisten werden nach dem Reißverschlussprinzip zusammengeführt.
Die jeweils ersten Elemente der Teillisten werden miteinander verglichen. Ist
so wird
an die nächste Stelle der neuen Gesamtliste gestellt. Ansonsten rutscht
nach, während
noch einmal mit dem nächsten Element von
also
verglichen wird. Das jeweils kleinere Element wird an das vorhergehende "aussortierte" hinten angestellt.
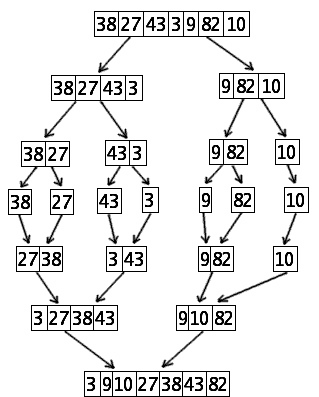
Datenfluss bei Mergesort
Funktionsorientierte Beschreibung
Die folgende Funktion teillisten2 ist der Prozedur teillisten aus Quicksort nachempfunden. Sie teilt die als Parameter übergebene Liste in der Mitte und erhält so 2 Teillisten, die gleich groß sind, bzw. bei einer ungeraden Anzahl an Elementen der Ausgangsliste, die linke Liste um 1 kleiner ist als die Rechte. Aufgrund von floor() funktioniert das, welches nur die Ganzzahl zurückgibt.
Die Prozedur führt jetzt beide sortierten Teillisten zusammen und bildet daraus die gesamte sortierte Liste.
Effizienzbetrachtung von Mergesort
Da Mergesort jede Liste, ob sortiert oder unsortiert, halbiert und abarbeitet, ist die Effizienz von Mergesort im best, worst und average case immer gleich. Es ergeben sich folgende Aufwandsbeziehungen
Wir nehmen vereinfachend an, dass die Anzahl der Elemente eine Zweierpotenz ist.
Durch Anwendung des zweiten Falles der Meistermethode ergibt sich folgende Lösung.
Binäres Suchen
Das Verfahren
Neben dem Sortieren von Schlüsseln ist das effiziente Suchen von großer Bedeutung, insbesondere für das Gebiet information retrieval ("Wiederauffinden/ Wiedergewinnung von Informationen"). Praktische Anwendungsgebiete für die binäre Suche sind Auskunftssysteme aller Art, wie zum Beispiel das Telefonbuch. Eine ineffiziente Suche kann viel Ressourcen in Anspruch nehmen. Um das aufwändige Umspeichern von Daten zu vermeiden, verwendet man eine Indexliste und Schlüssel zur Identifizierung von Datensätzen.
Die Suche von in einer aufsteigend sortierten Gesamtliste
erfolgt durch die Suche in den beiden Teillisten und
. Der Divide-Prozess der Zerlegung erfolgt mit
. Wir gehen vereinfachend davon aus, dass
eine Zweierpotenz ist. In der Implementation wird
verwendet.
Bei der Suche wird immer mit dem ersten Element
aus der rechten Teilliste
verglichen. Ist
ist die Suche bereits beendet. Ist
wird die Suche in der linken Teilliste
, ist
in der rechten Teilliste
fortgesetzt. Die Fortsetzung der Suche erfolgt jedoch nur, wenn die zu durchsuchende Liste nicht leer ist.
Funktionsorientierte Beschreibung mit Multiple-value-context
Effizienzanalyse
Die Länge der Teillisten wird in jedem Schritt halbiert, insbesondere wenn die Anzahl der Elemente von
eine Zweierpotenz ist. Die Anzahl der rekursiven Aufrufe entspricht der Anzahl der Halbierungsschritte, also
Stück. Setzt man für den in jedem Schritt stattfindenden Vergleich einen konstanten Aufwand
ein, erhält man den Gesamtaufwand
Dies trifft für den average case sowie für den worst case zu. Der best case benötigt nur einen einzigen Vergleich und arbeitet mit konstantem Aufwand , unabhängig von der Anzahl
.
Vergleich zur sequenziellen Suche
Es ist nur schwer zu erkennen, dass die Binärsuche effizienter sein soll, als die sequenzielle Suche von in einer aufsteigend sortierten Liste
.
Bei der sequenziellen Suche vergleicht man mit den aus
stammenden Elementen, beginnend beim Kleinsten. Dies wird so lange durchgeführt, bis
gefunden wurde. Würde man den Fall
miteinbeziehen, so könnte die Suche im Fall, dass das erste Element
größer ist als
, (erfolglos) beendet werden.
Wir gehen dabei wieder von paarweise verschiedenen Listenelementen aus:
Im Falle, dass gilt
. Das wäre ohne Frage der Best-Case. Im Worst- sowie im Average-Case werden
Durchläufe nötig, womit
gilt.
Sollte jedes Element aus
mit gleicher Wahrscheinlichkeit mit
übereinstimmen, so könnte man den Aufwand wie folgt beschreiben:
Damit ist klar, dass man der sequenziellen Suche die Binärsuche vorzieht.
Multiplikation großer ganzer Zahlen
Die Multiplikation großer ganzer Zahlen ist ein Verfahren, welches 1960 von Karatsuba und Ofman entwickelt wurde. Sie ist ein typisches Teile-und-Herrsche-Verfahren. Die Idee, die sich dahinter verbirgt, ist die Verringerung des Rechenaufwandes im Vergleich zu der Schulmethode, die mit einem quadratischen Aufwand arbeitet. Hierzu werden einige Multiplikationsvorgänge, die mit einem quadratischen Aufwand arbeiten durch Additionsverfahren und Verschiebungen, die linear arbeiten, ersetzt.
Wir verabreden zunächst, dass und
die gleiche Stelligkeit
haben und
eine gerade Zahl ist. Wir halbieren die beiden zu multiplizierenden Zahlen in einen High-Teil
und
und einen Low-Teil
und
. Es gilt somit
ist die Basis der Zahlendarstellung, z.B.
. Die beiden High- und Low-Teile sind infolge der Halbierung gleich lang.
Die Lösung der Multiplikation erfolgt mit
Auf diese Art und Weise entsteht die Multiplikation zweier -stelliger Zahlen durch 4 gleichartige Multiplikationen zweier
-stelliger Zahlen und drei Additionen maximal
-stelliger Zahlen. Der Aufwand der Addition beträgt
. Das ergibt einen Gesamtaufwand von
Die Anwendung der Meistermethode ergibt:
Im Vergleich zur Schulmethode ist das keine Verbesserung, da beide Verfahren mit quadratischem Aufwand arbeiten. Um eine Verbesserung zu erzielen, ist die Umformung von erforderlich.
Diese Umformung setzen wir in unsere Gleichung wieder ein. Es entsteht somit:
In diesem Ausdruck kommen zwei Produkte doppelt vor. Diese werden mit einem Aufwand von einmal berechnet und anschließend in die betreffenden Stellen nur noch eingesetzt.
Zu den beiden Multiplikationen von und
, kommt noch die Multiplikation von
, zwei je
-stelligen Zahlen sowie deren Addition (in
) hinzu.
Es ergibt sich somit ein Gesamtaufwand von
Die Anwendung der Meistermethode ergibt
Die Multiplikation zweier -stelliger Zahlen nach dieser Methode dauert somit ca. 5.2 Minuten (Nebenrechnung:
). Die gleiche Berechnung nach der Schulmethode dauert mehr als 1 Tag und 3 Stunden. (Nebenrechnung:
)
Ein kleines Beispiel
Wir wollen uns die Multiplikation großer ganzer Zahlen einmal am Beispiel anschauen.
Wir multiplizieren die Zahlen und
. Beide Zahlen sind 12-stellig.
ist somit
. Unsere Basis
Übung
Quellenverzeichnis
- Christian Wagenknecht: Algorithmen und Komplexität, Fachbuchverlag Leipzig, 2003,
- Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein: Algorithmen - Eine Einführung, Oldenbourg Verlag München Wien, 2. Auflage, 2007