P-NP-Problem und Näherungsverfahren
Aus ProgrammingWiki
Inhaltsverzeichnis |
P-NP
Einleitung
|
Ein zentrales Thema der Informatik ist es, für Probleme algorithmische Lösungen zu finden. Die Theoretische Informatik versucht dabei für ganze Problemklassen allgemeine Lösungen zu finden. Weiterhin ist es nicht zufriedenstellend nur irgendeine Lösung zu finden, die bestmögliche Lösung ist das Ziel. Die Bildung von solchen Problemklassen ist, wie bei jeder Klassenbildung, eine Verallgemeinerung: eine Reduzierung auf wesentliche relevante Merkmale. Ein solches Merkmal sollte bei den betrachteten Dingen sehr unterschiedlich ausgeprägt sein, um Kategorien/Klassen bilden zu können. Bei den Rest-Klassen in der Zahlentheorie z.B. werden Zahlen klassifiziert. Der Modulo bezüglich eines festgelegten Divisors ist das Klassifizierungsmerkmal. Es lassen sich also Klassen von Zahlen bilden, die ein gemeinsames Merkmal haben: den gleichen Rest bei einem bestimmten Divisor. Aber welches Merkmal weisen alle Probleme auf und könnte der Klassifizierung dienen? Das wohl relevanteste Merkmal eines jeden Problems ist der Aufwand den die Lösung des Problems erfordert. So ist die asymptotische Laufzeit eines problemlösenden Algorithmus eine Eigenschaft die zur Abgrenzung verwendet werden kann. Bei so abstrakten Dingen wie "Problemen" stellt sich außerdem die Frage ob diese überhaupt gleichartig und damit klassifizierbar sind. Es gibt verschiedene Arten von Problemen: Suchprobleme wie "Finde den Knoten mit dem größten Grad in einem Graphen" oder Optimierungsprobleme wie "Wieviele verschiedene Farben sind zur Einfärbung der deutschen Bundesländer mindestens notwendig" oder Entscheidungsprobleme wie "Ist ein Wort ein Palindrom". Aber alle Probleme lassen sich auf Entscheidungsprobleme zurückführen. Die Problemstellung wird unter Angabe der Lösung umformuliert. Also statt "Finde den Knoten mit dem größten Grad in einem Graphen!" wird "Ist im Graphen $G$ der größte Grad $5\:$?" gefragt. Das Ergebnis kann nur noch Ja oder Nein sein. Der zur Lösung des Problems erforderliche Algorithmus ist der Gleiche, nur erweitert um den Vergleich mit dem gefragten Ergebnis, welcher in Polynomialzeit erfolgt. Da die Gleichartigkeit nun festgestellt ist, müssen bei weitergehender theoretischer Betrachtung also nur Entscheidungsprobleme berücksichtigt werden, um pauschale Aussagen machen zu können. Außerdem erlaubt diese Feststellung, dass auf Entscheidungen basierende Konzepte wie Grammatiken und Automaten zulässige Hilfsmittel sind. |
- Zusammenfassung
- Bei der Problemklassifizierung werden Probleme nach ihrem Lösungsaufwand in Kategorien eingeordnet.
Die Klasse P
- Definition
- $\textbf{P}$ ist die Klasse aller Probleme, die mit deterministischen Algorithmen in polynomialer Zeit gelöst werden können.
- Deterministisch
- Der Algorithmus zur Lösung des Problems geht auf einem vordefinierten Weg zum Ziel und kann durch eine deterministische Turing-Maschine abgebildet werden.
- Polynomiale Zeit
- Es handelt sich hier nicht um eine absolute Zeit, sondern um das Verhalten der Laufzeit bei steigender Problemgröße. Wenn dieses Verhalten durch eine Polynomfunktion beschrieben werden kann, dann spricht man von "polynomialer Zeit".
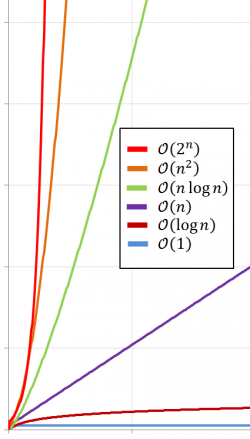
Mit Hilfe der Polynomfunktion wird also eine relative Zeiteinheit berechnet. Berechnet man diese für verschiedene Eingabegrößen ergibt sich der Laufzeitgraph.
Eine Polynomfunktion ist eine Funktion der Form:
.
Zur Bestimmung der relativen Zeit muss für $n$ die Problemgröße eingesetzt werden. Die Variablen $k$ und $a_i$ sind dabei abhängig vom jeweiligen Algorithmus.
Wenn die Laufzeit eines Algorithmus bezüglich einer Problemgröße $n$ mit einem solchen Polynom ausgedrückt werden kann, dann ist das entsprechende Problem der Klasse $\textbf{P}$ zuzuordnen.
Welche der folgenden Komplexitäten lassen auf Zugehörigkeit zur Klasse $\textbf{P}$ schließen?
| a) | $\mathcal{O}(1)$ |
| b) | $\mathcal{O}(n)$ |
| c) | $\mathcal{O}(log(n))$ |
| d) | $\mathcal{O}(\frac{2n}{n-1})$ |
| e) | $\mathcal{O}(n^2)$ |
| f) | $\mathcal{O}(n\:log(n))$ |
| g) | $\mathcal{O}(n^{1000000})$ |
| h) | $\mathcal{O}(1^n)$ |
- Zusammenfassung
- Durch die Klasse $\textbf{P}$ werden die praktisch effizient lösbaren Probleme zusammengefasst. Dazu wird eine obere Schranke in Form eines Polynoms definiert und Determinismus gefordert, so dass nur Probleme in die Klasse fallen, deren Aufwand im Verhältnis zur Problemgröße ein bestimmtes Maß nicht übersteigt.
Die Klasse EXPTIME
- Definition
- $\textbf{EXPTIME}$ ist die Klasse aller Probleme, die mit deterministischen Algorithmen in $\mathcal{O}(2^{p(n)})$ gelöst werden können, wobei $p(n)$ eine Polynomfunktion von $n$ ist.
Da es nur eine obere Grenze gibt, ist die Klasse $\textbf{EXPTIME}$ eine Übergruppierung. Das bedeutet, dass $\textbf{P}$ in $\textbf{EXPTIME}$ enthalten ist. $\textbf{P}$ ist dabei eine echte Teilmenge ($P\subset \textbf{EXPTIME}$), denn $\textbf{P}$ ist nach oben begrenzt und es existieren nachweislich Probleme die nur von Algorithmen mit Aufwänden oberhalb dieser Schranke gelöst werden können.
- Beispiel
- Prüfung ob ein beliebiger Boolescher Ausdruck wahr sein kann
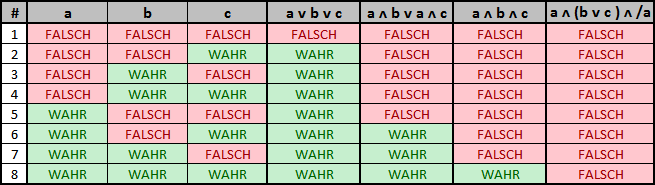
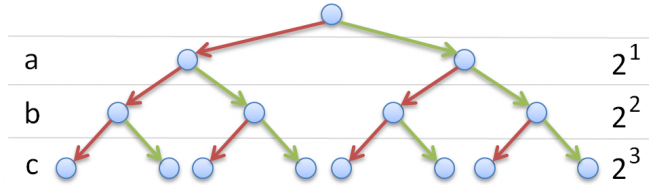
Es müssen im schlimmsten Fall alle möglichen Belegungen ($2^n$ Stück) geprüft werden, um zum Ergebnis zu gelangen.
Für Probleme die einen höheren Aufwand als den exponentiellen für ihre Lösung erfordern, können beliebig Klassen der Form $\textbf{X-EXPTIME}$ formuliert werden. Probleme mit doppelt exponentiellen Aufwand (bis $\mathcal{O}(2^{2^{p(n)}})$) werden so der Klasse $\textbf{2-EXPTIME}$ zugeordnet. Analog kann die Klassenformulierung für höhere Aufwände nach dem gleichen Schema fortgesetzt werden. Die jeweilige Klasse wird in entsprechender Exponentationsstufe immer durch eine Polynomfunktion von $n$ nach oben begrenzt.
- Zusammenfassung
- Alle lösbaren Probleme werden durch die $\textbf{EXPTIME}$-Klassen abgedeckt. $\textbf{P}$ ist eine echte Teilmenge von $\textbf{EXPTIME}$.
Durch die Klassen $\textbf{EXPTIME}$ und $\textbf{P}$ sind alle lösbaren Problem im Prinzip vollständig klassifiziert. Eine weitere Klasse zwischen $\textbf{EXPTIME}$ und $\textbf{P}$ kann jedoch nicht mehr über den rein deterministischen Aufwand zur Problemlösung gebildet werden. Um trotzdem die "einfachereren" von den "schwierigen" $\textbf{EXPTIME}$-Problemen abzugrenzen wird ein weiteres Merkmal zur Klassifizierung herangezogen: der Nichtdeterminismus.
Die Klasse NP
- Definition
- $\textbf{NP}$ ist die Klasse aller Probleme, die mit nichtdeterministischen Algorithmen in polynomialer Zeit gelöst werden können.
- Nichtdeterministisch
- Ein nichtdeterministischer Algorithmus probiert mehrere verschiedene Wege zur Bestimmung der Lösung und kann durch eine nichtdeterministische Turing-Maschine abgebildet werden.
Nichtdeterminismus wird bei der Programmierung durch Parallelisierung und Backtracking umgesetzt. Die für $\textbf{NP}$ geforderte polynomiale Zeit bezieht sich dabei nur auf einen der vielen parallelen Verarbeitungswege. Es geht also um die Zeit die der Algorithmus benötigen würde, wenn er bei der Suche nach der Lösung in keine Sackgasse geraten würde und somit einen deterministischen Weg zur Lösung verfolgt hätte. Obiges Beispiel zeigt ein solches $\textbf{NP}$ Problem. Die Prüfung einer Kombination die wahr ist, ist in Polynomialzeit machbar. Jedoch die Anzahl der zur Prüfung aller möglichen Kombinationen benötigten parallelen Verarbeitungen ist exponentiell.
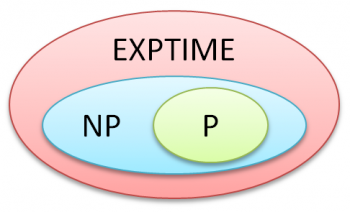
Die reine Zugehörigkeitsbeziehung zu den Klassen $\textbf{P}$ und $\textbf{EXPTIME}$ lässt sich in einem Venn-Diagramm darstellen. Dass $\textbf{P}$ eine echte Teilmenge von $\textbf{EXPTIME}$ ist, wurde bereits klar gestellt. $\textbf{P}$ ist auch eine Teilmenge von $\textbf{NP}$, denn jeden deterministischen Algorithmus kann man in einen nichtdeterministischen Algorithmus überführen.
Das besondere an nichtdeterministische Algorithmen mit polynomialer Laufzeit ist, dass der Weg zum echten deterministischen Algorithmus mit polynomialer Laufzeit recht kurz ist. Man müsste "nur" wissen welcher der richtige Weg zum Ziel ist, also wissen wie das "Orakel" funktioniert.
Ob es so eine Methode geben kann, ist eine der derzeit wichtigsten Fragen der theoretischen Informatik.
Offene Fragen
Die wirklichen Grenzen der Klasse $\textbf{NP}$ sind derzeit noch unbekannt. Damit einhergehend wird ihre ganze Daseinsberechtigung in Frage gestellt.
- Frage 1
- $\textbf{NP}=\textbf{EXPTIME}$
Dass es Probleme gibt, die derzeit nur mit exponentiellem Aufwand deterministisch gelöst werden können, ist belegt. Ebenso, dass einige dieser Probleme nichtdeterministisch in Polynomialzeit gelöst werden können. $\textbf{NP}$ ist damit auf jeden Fall eine Teilmenge von $\textbf{EXPTIME}$. Unbekannt ist, ob sich nicht für jedes $\textbf{EXPTIME}$-Problem ein nichtdeterministisch arbeitender Algorithmus finden lässt, dessen Laufzeit polynomial ist. Höchstwahrscheinlich ist dem nicht so. Aber selbst wenn sich diese Möglichkeit bewahrheiten würde, wären die Konsequenzen nur theoretischer Natur. Die praktische Laufzeit der gefundenen nichtdeterministischen Algorithmen zur Lösung eines $\textbf{EXPTIME}$-Problems würde sich kaum ändern.
Ganz anders ist es bei der nächsten Frage.
- Frage 2
- $\textbf{P}=\textbf{NP}$
Dass für jedes $\textbf{P}$ Problem auch ein nichtdeterministischer Algorithmus angegeben werden kann, ist klar. Damit ist $\textbf{P}$ definitiv eine Teilmenge von $\textbf{NP}$. Ob aber für jedes $\textbf{NP}$-Problem ein deterministischer Polynomialzeit-Algorithmus gefunden werden kann, wird stark bezweifelt (Cook'sche Vermutung). Es würde bedeuten, dass man die Aufgabe des "Orakels" in Polynomialzeit lösen könnte. Bis heute ist es jedoch nicht gelungen für auch nur ein einziges nachweislich in $\textbf{NP}$ liegendes Problem einen deterministischen Algorithmus anzugeben, der das Problem in Polynomialzeit löst. Diese Fragestellung ist unter dem Namen P-NP-Problem bekannt geworden.
Im Jahr 2000 hat das Clay Mathematics Institute in Cambridge ein Preisgeld von 1 Million Dollar für die Lösung von einem der sogenannten Millenium Probleme ausgelobt. Eines der 7 Probleme wurde 2002 bereits gelöst.
Die Lösung des P-NP-Problems steht noch aus: http://www.claymath.org/millennium-problems/p-vs-np-problem
Polynomiale Reduktion
- Definition
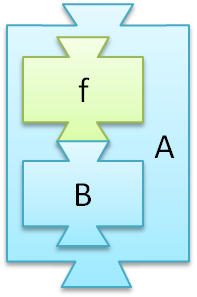
- Ein Problem $A$ ist polynomial reduzierbar auf ein Problem $B$, geschrieben $A\:\leq_p\:B$, wenn es eine Funktion $f: A \rightarrow B$ gibt, die alle Probleminstanzen von $A$ zu Probleminstanzen von $B$ umrechnet und in Polynomialzeit ausgeführt werden kann.
|
Abstrakt betrachtet geht es um nichts anderes als die Feststellung, dass Problem $A$ nur ein "Spezialfall" von Problem $B$ ist. Da die Probleme $A$ und $B$ Entscheidungsprobleme sind, kann man sie auch als Wortprobleme der formalen Sprachen auffassen. Lassen sich alle Wörter der Sprache $L_A$ zu Wörtern der Sprache $L_B$ in polynomialer Zeit umformen, dann ist $A$ polynomial reduzierbar auf $B$. Die für diese Umformung erforderliche Zeit ist hierbei entscheidend. Die Aufwände zur Lösung von $B$ und für die Ausführung von $f$ müssen addiert werden um den Aufwand zur Lösung von $A$ zu bestimmen. Durch die Abgeschlossenheit der Polynome bezüglich Addition bleibt bei polynomialem Aufwand für $f$ der Gesamtaufwand bei dem zur Lösung von $B$. Die Problemklassifizierung von $B$ kann also direkt auf $A$ übertragen werden:
Im Umkehrschluss, lassen sich dadurch ebenso Klassenzugehörigkeiten ausschließen:
|
Das Symbol $\leq_p$ soll nahe legen, dass $A$ "einfacher" als $B$ ist (nicht weniger aufwendig). Denn um $A$ zu lösen benötigt man nur ein Transformation zusammen mit der vorhandenen Lösung für $B$ und wenn $A$ nur ein "Spezialfall" von $B$ ist, dann ist $B$ das allgemeinere, umfassendere Problem. Könnte man alle Probleme aus $\textbf{NP}$ mittels polynomialer Reduktion auf ein einziges zurückführen, dann hätte man ein Basis-Problem auf das man sich bei der Lösungsoptimierung konzentrieren kann.
NP-Schwere (NPH) und NP-Vollständigkeit (NPC)
- Definition
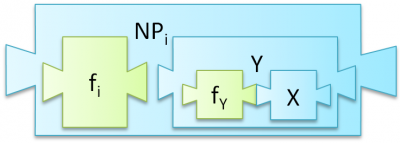
- Ein Problem $X$ heißt $\textbf{NP}$-schwer, wenn alle Probleme aus $\textbf{NP}$ auf $X$ polynomial reduziert werden können.
|
Auf den ersten Blick scheint die Prüfung eines Problems $X$ auf $\textbf{NP}$-Schwere recht umfangreich zu sein, denn es gibt zahlreiche Probleme in $\textbf{NP}$ deren polynomiale Reduzierbarkeit geprüft werden müsste. Wenn man allerdings bereits ein nachweislich $\textbf{NP}$-schweres Problem $Y$ hat, reicht es aufgrund der Transitivität von $\leq_p$ aus, $Y\:\leq_p\:X$ nachzuweisen.
Denn wenn $Y$ $\textbf{NP}$-schwer ist, dann müssen alle $\textbf{NP}$ Probleme auf $Y$ polynomial reduzierbar sein. Und wenn $Y$ auf $X$ polynomial reduziert werden kann, dann können, über den Umweg $Y$ auch alle $\textbf{NP}$ Probleme auf $X$ reduziert werden. |
Die Frage die sich stellt, ist: Woher nehme man das erste $\textbf{NPH}$ Problem von dem man ableiten kann?
- Definition
- Ein Problem $X$ heißt $\textbf{NP}$-vollständig, wenn es $\textbf{NP}$-schwer ist und in der Klasse $\textbf{NP}$ liegt.
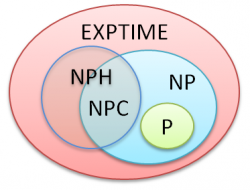
Die Definition der $\textbf{NP}$-Vollständigkeit erfordert also die Definition der $\textbf{NP}$-Schwere. Unter der Annahme, dass $\textbf{P} \neq \textbf{NP}$ und $\textbf{EXPTIME} \neq \textbf{NP}$, ergibt sich folgendes Venn-Diagramm zur Beschreibung der verschiedenen Problemklassen.
|
$\textbf{NPC}$ Probleme sind damit die schwierigsten aber auch am erfolgversprechendsten Probleme, deren Lösung große Auswirkungen hätten. Als $\textbf{NP}$-Problem gilt es "nur noch" den Nichtdeterminismus zu überwinden und als $\textbf{NPH}$ Problem würde diese Lösung gleichzeitig alle anderen $\textbf{NP}$-Probleme lösen.
Um ein neues Problem auf $\textbf{NP}$-Vollständigkeit zu prüfen, muss zunächst geprüft werden ob es sich um ein $\textbf{NP}$-Problem handelt. Ist dies nachgewiesen, kann die Polynomiale Reduktion angewendet werden. Lässt sich also ein bekanntes $\textbf{NPC}$-Problem auf das neue Problem polynomial reduzieren, dann muss das neue Problem auch ein $\textbf{NPC}$-Problem sein.
- Satz von Steven A. Cook
- Das Erfüllbarkeitsproblem der Aussagenlogik (SAT) ist $\textbf{NP}$-vollständig.
Bei dem SAT-Problem handelt es sich um das Beispiel aus dem Kapitel Die Klasse EXPTIME. Wie bereits erwähnt, geht es darum herauszufinden ob eine beliebige aussagenlogische Formel wahr sein kann. Steven A. Cook hat 1971 nachgewiesen, dass es sich um ein $\textbf{NP}$-schweres Problem handelt. Da das SAT-Problem selbst ein $\textbf{NP}$-Problem ist, ist es sogar $\textbf{NP}$-vollständig.
Da Cook kein anderes $\textbf{NP}$-schweres Problem hatte auf das er das SAT-Problem reduzieren konnte, musste er alle $\textbf{NP}$-Probleme darauf reduzieren. Um nicht alle $\textbf{NP}$-Probleme einzeln prüfen zu müssen, verwendete er eine Eigenschaft von nichtdeterministischen Algorithmen die alle $\textbf{NP}$-Probleme gemeinsam haben. Allesamt lassen sie sich durch eine nichtdeterministische Turing Maschine beschreiben. Cook gelang es die Funktionsweise einer Turing Maschine mit ausschließlich aussagenlogischen Formeln zu beschreiben.
Da jeder nichtdeterministische Algorithmus eines dazugehörigen $\textbf{NP}$-Problems mit einer Turing Maschine (als Akzeptor) dargestellt werden kann und jede Turing Maschine durch eine aussagenlogische Formel, ist jede $\textbf{NP}$-Probleminstanz nur eine "spezielle" aussagenlogische Formel. Die Funktion zur Überführung einer beliebigen $\textbf{NP}$-Probleminstanz über dessen Turing Maschine zur aussagenlogischen Formel ist mit $\mathcal{O}(n^3)$ nach oben beschränkt und erfüllt damit alle Vorraussetzungen einer polynomialen Reduktion.
- Zusammenfassung
- Von den schwierigen Problemen (aus der Klasse $\textbf{EXPTIME}$) lassen sich all die Probleme, die durch einen nichtdeterministischen Algorithmus in Polynomialzeit gelöst werden können ($\textbf{NP}$), auf alle $\textbf{NPC}$ Probleme zurückführen. Eine Verbesserung des Algorithmus zur Lösung eines $\textbf{NPC}$ Problems verringert damit automatisch die Aufwände aller $\textbf{NP}$-Probleme und aller $\textbf{NPH}$-Probleme die auf dieses $\textbf{NPC}$ Problem reduziert werden können.
Es sind mehr als 1000 solcher $\textbf{NPC}$ Probleme bekannt. Einige davon werden im Folgenden thematisiert.
Pseudopolynomialität
Das Rucksackproblem scheint auf den ersten Blick mit dynamischer Programmierung in Polynomialzeit lösbar zu sein.
Bei Betrachtung der Implementation findet man:
- Eine for-Schleife zur Initialisierung des Array $\mathcal{O}(n+1)$ (vernachlässigbar, da es eine Eigenart von Javascript ist, dass man mehrdimensionale Arrays nicht mit einem einzigen Aufruf erzeugen kann)
- Eine äußere for-Schleife über die Anzahl der Gegenstände $\mathcal{O}(n)$
- Eine innere for-Schleife über Anzahl der möglichen Gewichte $\mathcal{O}(max)$
Es ergibt sich damit eine Laufzeit von $\mathcal{O}(n) \dot{} \mathcal{O}(max) = \mathcal{O}(n \dot{} max)$, was zunächst polynomial erscheint.
Der Irrtum liegt in der Betrachtung von $max$ als Konstante. Bei der Worst-Case-Betrachtung kann $max$ jeden beliebigen Wert annehmen. Somit kann man ihn auch in Abhängigkeit von $n$ definieren, z.B. $max = 2^n$
Es ergibt sich damit eine Komplexität von $\mathcal{O}(n \dot{} 2^n)$ welche nicht mehr polynomial begrenzt ist.
Beispiele
SAT-Problem
Das SAT-Problem ist ein Entscheidungsproblem. Gegeben ist eine aussagenlogische Formel. Jetzt ist die Frage, ob diese erfüllbar ist. Dazu muss die Formel $F$ allgemeingültig sein $\leftrightarrow$ $\neg F$ nicht erfüllbar.
Aufbau eines Terms:
- Variablen: $x_1$, $x_2$, ...., $x_n$
- Operationszeichen: $\wedge$ und $\vee$
- Negation: $\neg$
Beispiele
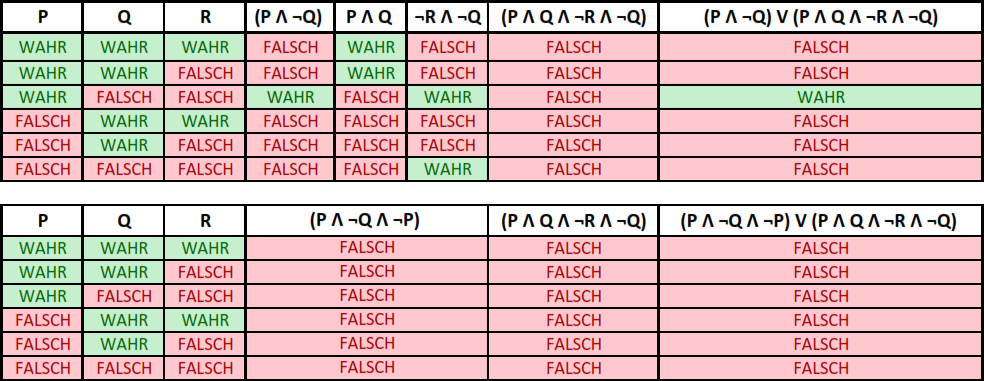
$(P \wedge \neg Q) \vee (P \wedge Q \wedge \neg R \wedge \neg Q)$
$(P \wedge \neg Q \wedge \neg P) \vee (P \wedge Q \wedge \neg R \wedge \neg Q)$
Zur Visualisierung kann eine Wahrheitstabelle verwendet werden. Diese kann nicht in Polynomialzeit deterministisch aufgestellt werden.
SAT-Varianten
- 3-SAT - Formel $F$ enthält höchstens 3 verschiedene Literale
- MAX-SAT - Formel $F$ mit der maximale Anzahl erfüllbarer Klauseln gesucht
Satz von Cook und Levin
1971 begründete Cook die neue Komplexitätsklasse $NP$. Er fand heraus, dass es eine Unterklasse in $NP$ gibt ($NP$-vollständig), auf die alle $NP$-Probleme zurückgeführt werden können und dass das SAT-Problem in diese Klasse gehört. Unabhängig davon fand 1973 der Ukrainer Leonid Levin einen vergleichbaren Satz heraus. Cook erhielt dafür 1982 den Turing-Award.
Karps vollständige Probleme
1972 erprobte er verschiedenste Probleme mit dem Satz von Cook in die Klasse $NPC$ einzugliedern. Daraus entstand eine Liste mit 21 Problemen, die die zugehörige Reduktion beinhaltet.
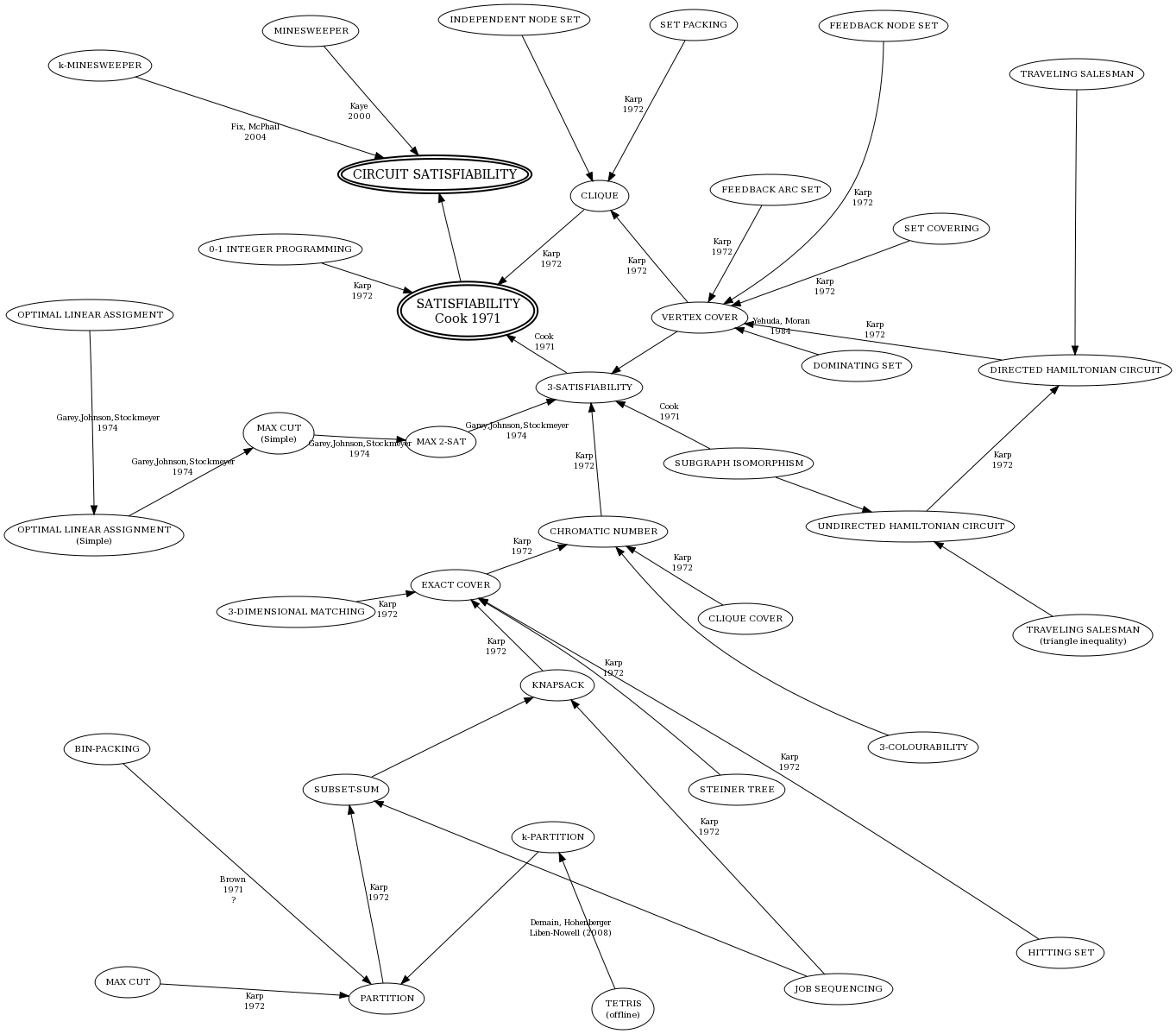
Cliquenproblem
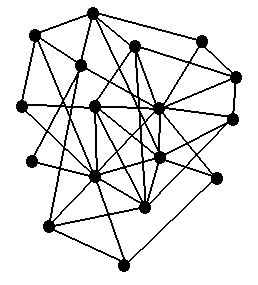
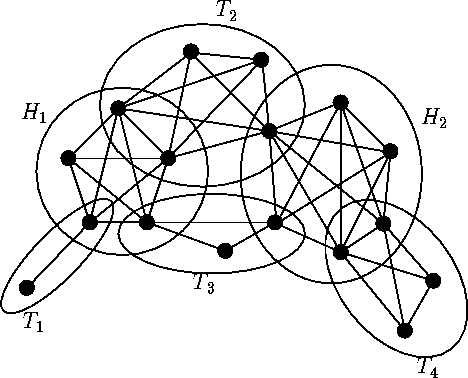
Das Cliquenproblem gehört zu den klassischen $NP$-vollständigen Problemen (siehe Karps Liste). Wir haben einen zufälligen ungerichteten Graphen $G$. Dieser besteht aus der Knotenmenge $V$ und den Kanten $E$. Die Knoten sind zufällig miteinander verbunden. Eine Clique ist ein Menge von Knoten, die vollständig untereinander verbunden sind. Man unterscheidet in 2 Problemfälle. Das Entscheidungsproblem befasst sich mit der Frage, ob es in dem Graphen $G$ eine Clique mit der Anzahl der Knoten $k$ gibt. Das Optimierungsproblem ist die Frage nach der maximalen Größe von $k$ in einem Graphen $G$.
Überführung SAT- zu Cliquenproblem
Wir wollen eine Formel $F$, wie sie bei einem SAT-Problem vorgegeben ist zu einem ungerichtete Graphen $G$ transformieren. Dazu ergibt sich aus jeder Variable der Formel $F$ ein Knoten des Graphen. Die Verbindung der Knoten wird durch folgenden Regeln begrenzt:
- Die Verbindung von Punkten, die im gleichen Disjunkten-Term stehen ist verboten.
- Die Verbindung zueinander negierter Variablen ist verboten.
Die Formel $F$ ist erfüllbar, wenn sie durch eine n-Clique abgebildet werden kann. Dies Formel $F$ ist dann erfüllt, wenn die vorkommenden Knoten in einer Clique true ergeben.
Beispiel
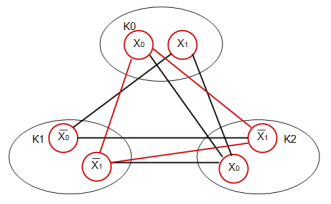
$$f = (x_0 \vee x_1) \wedge (\neg x_0 \vee \neg x_1) \wedge (x_0 \vee \neg x_1)$$ Dieser Term besteht aus 3 Disjunkten Termen. Wir nennen sie $K_0$, $K_1$ und $K_2$. Somit ergibt sich die Anzahl der Cliquen $k = 3$ Mit dieser Vorgabe entwickeln wir den Graph. Achten dabei auf die Regeln mit der die Punkte verbunden werden dürfen. Zum Abschluss suchen wir in der Menge der gerade eingezeichneten Kanten einen Kreis, der alle Cliquen miteinander verbindet.
Anhand dieses Kreises können wir die Belegung der Variablen bestimmen. Somit hätten wir bewiesen, dass Ein SAT-Problem in ein Cliquenproblem reduziert werden kann.
Euler-Kreis-Problem
Das Euler-Kreis-Problem befasst sich mit dem Finden eines Eulerkreises in einem Graphen $G$. Ein Eulerkreis ist ein Teilgraph des Graphen $G$ der alle Kanten genau einmal durchläuft.
Hamilton-Kreis-Problem
Das Hamilton-Kreis-Problem ist eines der 21 $NP$-vollständigen Probleme von Karps Liste. Es kann über das Cliquenproblem zu einem SAT-Problem reduziert werden.
Näherungsverfahren
Motivation
Es gibt viele Probleme, die praktische Bedeutung haben, jedoch NP-vollständig sind. Das wiederum bedeutet, dass es aussichtslos ist für diese Probleme die exakte Lösung in Polynomialzeit zu finden. Ein Beispiel hierfür ist das TSP. Die Relevanz dieser Probleme ist aber so groß, das man nach Möglichkeiten sucht sie zu lösen. Im Wesentlichen gibt es drei Ansätze um NP-vollständige Probleme zu lösen.
Erstens ein Algorithmus mit exponentieller Laufzeit kann genutzt werden wenn die Problemgrößen so klein sind, dass der hierfür benötigte Zeitaufwand noch polynomial ist.
Zweitens kann es sein, dass man wichtige Spezialfälle findet, die in polynomialer Zeit lösbar sind.
Drittens ist es möglich eine fast optimale Lösung in polynomialer Zeit zu finden.
Diese fast optimalen Lösungen genügen oftmals in der Praxis. Ein Algorithmus, welcher eine fast optimale Lösung liefert nennt man Näherungsalgorithmus oder Approximationsalgorithmus.
Optimierungsproblem
- Definition
- Ein $\textbf{Optimierungsproblem}$ ist ein 4-Tupel mit folgenden Eigenschaften.
- 1. $\mathcal{D}$: ist die Menge der Eingaben.
- 2. $S(I) \text{ für } I \in \mathcal{D}$: ist eine Funktion die, die Menge der zu $I$ zulässigen Lösungen angibt.
- 3. $f:S(I) \to \mathbb{N}^{\neq 0}$: Die Bewertungs- oder Maßfunktion.
- 4. Ziel $\in \{min, max\}.$
Beispiel für das TSP:
???
Approximationsalgorithmus
- Definition
- Gegeben sei ein Optimierungsproblem. Ein Approximationsalgorithmus A berechnet zur Eingabe $I \in \mathcal{D} $ in Zeit $t(\vert{I}\vert) $ eine Ausgabe $\sigma_{I}^{A} \in S(I)$. Man schreibt $A(I) = f(\sigma_{I}^{A})$.
Um die Güte eines Algorithmus beschreiben zu können ist es wichtig bestimmte Grenzen anzugeben um sie mit dem Optimum zu vergleichen, falls es möglich ist. Diese Grenzen werden als obere und untere Schranke angegeben. Folgender Ausdruck gibt die Schranken des Algorithmus an $\sigma_{I}^{A}$. $I$ steht hier für eine untere schranke des Algorithmus und nicht des Problems. $A$ bezeichnet eine obere Schranke der Lösung des Algorithmus, wie weit kann er höchstens daneben liegen. Es gibt viele Approximationsalgorithmen und algorithmische Ansätze, für die noch niemand Aussagen über die Qualität getroffen hat. Hierfür gibt es zwei Gründe geben entweder es ist noch niemandem gelungen oder der Algorithmus liefert beliebig schlechte Lösungen.
Lokale Suche
Motivation
Bei vielen technischen Problemen, auch bei Problemen allgemeiner Natur, geht es oft darum ein Minimum oder Maximum zu bestimmen. Diese Aufgaben sind bereits aus der Schule bekannt. Man hat eine Funktion vorgegeben wie zum Beispiel $y=2x^4+x^2$. Die Funktion war vollständig bekannt, jetzt war es ein leichtes Nullstellen, Minima und Maxima zu finden.
In der Praxis sieht der Sachverhalt oft ganz anders aus. Hier gibt es keine fertigen Formeln zur Berechnung der Extremstellen. Unter Umständen können wir die Formel gar nicht ableiten, weil sie nur als Menge von Messdaten angegeben ist. Hierbei kommt der Aspekt der lokalen Suche zum tragen, weil keine globalen Kenntnisse über die Funktion vorhanden sind. Man muss also mit den zur Verfügung stehenden lokalen Information, damit sind die Messwerte gemeint, auskommen.
Heuristiken
- Definition
- $\textbf{Heuristiken}$ sind durch Erfahrung gewonnene Regeln und Verfahren, die in akzeptabler Zeit zu einer zufriedenstellenden Lösung führen. Man weiß zwar nicht, ob die gefundene Lösung optimal ist, man ist aber mit dem Ergebnis zufrieden, wenn sich abschätzen lässt, wie gut oder wie schlecht die gefundene Lösung ist. Durch Probieren wird versucht das Ergebnis weiter zu verbessern. Es handelt sich um Faustregeln oder Handlungsempfehlungen, basierend auf intuitiven Regeln. Aus einer Vielzahl von Möglichkeiten werden einige herausgefiltert.
Heuristiken sind von Nutzen, wenn man NP-vollständige Probleme in Polynomzeit lösen will. Weitere NP-vollständige Probleme sind: das SAT-Problem und das Cliquen-Problem.
- Frage?
- Nennen sie einige Heuristiken für das TSP!
- Zusammenfassung
- Heuristiken sind Algorithmen die ein Problem, zum Beispiel ein NP-volllständiges Problem näherungsweise lösen können. Das Lösungsverfahren liegt dabei in der Aufwandsklasse P, so dass das Ergebnis in akzeptabler Zeit berechnet werden kann. Hierfür nimmt man jedoch in Kauf, dass das gefundene Ergebnis nicht exakt ist.
weitere Algorithmen für die Lokale Suche
Verzweigen und Begrenzen
Branch and Bound (Verzweigen und Beschränken) ist eine Näherungslösung für ein Optimierungsverfahren. Nähere Informationen finden Sie hier.
Das Travelling Salesman Problem (TSP, deutsch: Rundreiseproblem) ist ein Problem der Graphentheorie. Es wird die kürzeste Rundreise durch alle $n$ Städte gesucht, ohne eine Stadt mehrfach zu besuchen. Dieses Problem findet heutzutage in der Logistik große Aufmerksamkeit. Weitere Informationen finden Sie hier.
Um Branch and Bound auf das TSP anzuwenden, benötigen wir eine Bewertungsfunktion. Diese wird zur Bound-Bestimmung der Knoten benutzt. Wir bauen eine untere Schranke $s_k$ für den Knoten $k$. Diese Schranke verhindert, dass wir einen kürzeren Weg finden und diesen nicht in unser TSP einbauen. Wenn wir im Graphen einen anderen Knoten finden, der eine kleinere untere Schranke besitzt ist dieser Knoten natürlich vorzuziehen. Der zurückgelegte Weg bis dahin ist dann ein potenzieller Anfangsweg des gesuchten minimalen Weges. Eine solche Schranke kann aus der aktuellen Teilweglänge vom Startpunkt und der Entfernung zum nächstgelegenem unbesuchten Knoten bestehen. Diese Schranke kann unter Umständen recht wenig bieten. Lokale Entscheidungen können das System stark ins Wanken bringen. Beispielsweise finden wir einen nächstliegenden Nachbarknoten mit sehr geringem Weg. Diesen müssten wir in unser TSP einbauen. Leider ist der Weg zu dem Knoten sehr lang, wodurch die Entscheidung diesen kurzen Weg zu nehmen, nicht die beste Entscheidung ist.
Es muss also der Weg von jedem Knoten bis zum kürzesten Weg mit in die Betrachtung einfließen. Wir nehmen dazu die Summe aller zu $k$ hin- und wegführenden Kanten und Teilen sie durch 2. Dadurch vermeiden wir eine Doppelzählung. Dieses Verfahren ist aber nur eine Heuristik. Wir erhoffen uns also eine schnelle Ergebnisfindung. Das Ergebnis kann demzufolge nur eine Näherungslösung sein.
Zu jeder Entfernungsmatrix kann eine zeilenreduzierte Entfernungsmatrix aufgestellt werden, bei der jede Zeile um das Zeilenminimum vermindert wird. Danach muss in jeder Zeile mindestens eine 0 stehen. Dies ist die Länge des kürzesten Weges in der reduzierten Entfernungsmatrix. Dies ist eine mögliche Lösung des TSPs, welche mit einer reduzierter Entfernungsmatrix berechnet wurde.
Hill climbing Algorithmus
Hill climbing ist eine Heuristik die ebenfalls unter dem Namen local search bekannt ist. Dieses Verfahren stellt eine einfache lokale Verbesserungsstrategie dar. Der Der Algorithmus arbeitet mit einem aktuellen Zustand und bewegt sich im allgemeinen nur zu den Nachbarn dieses Zustandes. Der Algorithmus erwartet bereits einen Lösungsvorschlag, welcher durch Modifikation besser werden soll. In vielen Fällen leitet eine Greedy-Heuristik eine Vorarbeit in dem sie eine Lösung erstellt.
Prinzipielles Vorgehen des Verfahrens
- Hill climbing kann man ins Deutsche mit Bergsteigen übersetzen. Diese Vorstellung des einen Berg hoch zu fahren, klettern bzw. steigen kann hier wörtlich genommen werden. Man stelle sich folgendes Szenario vor: ein Autofahrer möchte den Gipfel eines Berges erreichen, die Sicht ist stark eingeschränkt. Er kann nur die lokal zur Verfügung stehenden Weggabelungen einsehen.
- Frage
- Nach welchem Kriterium geht er vor wenn er den Gipfel erreichen will?
- Wenn sich der Autofahrer nun an diese Regel hält kann er auf den Gipfel kommen. Aber es kann auch sein das er einen nahe gelegenen Nebengipfel erreicht. Schon anhand dieser Illustration lässt sich erkennen, dass es sich hierbei um ein Verfahren handelt, welches ein lokales Optimum findet, dieses kann jedoch stark vom globalen Optimum abweichen.
Hill climbing am Beispiel des TSP
- Voraussetzung
- Man hat zu einem TSP eine bestehende Rundreise ermittelt.
- Vorgehen
Wähle zwei nicht benachbarte Knoten und überprüfe ob diese Kante, zwischen den zwei nicht benachbarten Knoten, günstiger ist als der bisherige Weg zwischen diesen Knoten.
Wenn ja dann füge diese Kante hinzu.
Pseudocode
CurrentState = Initialisierung();
repeat {
NeighborState = ein höchstwertiger Nachbar von CurrentState;
if (Value[Neighborstate] <= Value[CurrentState])
return CurrentState;
else
CurrentState = Neighborstate;
}
Probleme
- Die hill climbing Heuristik hat das Problem das sie stecken bleiben kann, hierfür kann es zwei Gründe geben.
- 1. Es wird ein lokales Optimum gefunden.
- 2. Es wird ein Plateau gefunden was nicht mehr verlassen werden kann.
Simulated Annealing
Um dieses Steckenbleiben zu vermeiden wurde von S. Kirkpatrick et. al. 1983 die Methode des simulierten Ausglühens entwickelt. Es handelt sich um ein Prinzip aus der Metallurgie bei dem nach Erhitzen eines Metalls eine langsame Abkühlung dafür sorgt, dass die Atome genügend Zeit haben sich in einer stabilen Kristallform anzuordnen. Hierbei wird ein energiearmer Zustand nahe am Optimum erreicht. Somit stellt dieses Verfahren eine weitere Verbesserungsstrategie dar, ähnlich wie das hill climbing. Hierbei wird ein natürlicher Vorgang in der Informatik abstrahiert und entsprechend umgesetzt.
- Die Analogie zur Informatik beruht auf der Tatsache, dass die Energie durch eine Kostenfunktion von verschiedenen Parametern beschrieben werden kann.
Vorgehen
Anstatt einen Lösungsvorschlag generell zu verbieten, wenn er nicht über einer gewissen Schwelle liegt, wird zufällig entschieden ob der Vorschlag nicht doch gültig ist. Hierbei hängt die zufällige Entscheidung von der Abweichung zu dieser Schwelle ab. Es gilt, dass kleinere Verschlechterungen eher zugelassen werden als größere. Auf lange Zeit gesehen, ist es jedoch möglich, dass sogar sehr große Abweichungen zugelassen werden. Dieses Zulassen von großen Abweichungen sorgt dafür, dass ein lokales Optimum wieder verlassen werden kann.
Pseudocode
procedure Metropolis(T)
begin
repeat /*gegenwärtiger Zustand ist i*/
gehe von i in neuen Zustand j über;
berechne die Differenz;
if $\triangle E_{ij} \leqq 0$ then akzeptiere Zustand j
else akzeptiere j mit Wahrscheinlichkeit
$p= e^{-\frac{\triangle E_{ij}}{T}}$
if j akzeptiert then i = j
until Gleichgewichtszustand für Temperatur T erreicht
end
Verbesserungen
Das Verfahren bleibt nicht mehr auf einem lokalen Optimum stecken, jedoch kann es relativ lange Zeit benötigen um es zu verlassen.
Merke
- Approximationsalgorithmen liefern zum Teil keine guten Ergebnisse, um jedoch näher an das Optimum heranzukommen, werden Verbesserungsstrategien eingesetzt. Diese Optimierungsalgorithmen verbessern also die Resultate von Approximationsalgorithmen.
- Diese Verfahren haben sich an technischen Prozessen orientiert, aufgrund der rasanten Weiterentwicklung ist es das sie nun ein eigenes Themengebiet in der Informatik bilden und nur noch wenig mit der ursprünglichen Thematik verbindet.
DNA computing und evolutionäre Algorithmen
Hierbei orientiert man sich am Verhalten der Natur um Lösungen für bestimmte Probleme zu finden. In der Natur wurden und werden viele Probleme durch die Evolution gelöst. Dabei überlebt die viel versprechenste Variation, auf lange Sicht. Diesen Prozess macht man sich in der Informatik zu nutze indem man ihn nachbildet und bestimmte Anpassungen vornimmt.
Biologische Grundlagen
- Definition
- Die $\textbf{Evolution}$ beschreibt einen Vorgang, nämlich die Weiterentwicklung von Organismen um sich an bestimmte Umstände anzupassen.
Charles Darwin war einer der Pioniere, er stellte als erster den Vorgang der natürlichen Selektion dar. Nach diesem haben Individuen, einer gewissen Population, Vorteile wenn sie entsprechend an Ihre Umgebung angepasst sind. Auf Grund ihrer Anpassung haben sie bessere Überlebenschancen. Dies führt dazu das auf lange Sicht, diese Merkmale der besser angepassten Individuen weiter vererbt werden. Nach einer gewissen Zeit hat sich dann diese Anpassung durchgesetzt.
Der menschliche Körper besteht aus vielen differenzierten Zellen. Die Tatsache das im Körper ständig katabole und anabole Prozesse im Gang sind, ist der Grund dafür das bestimmte Zellen, Gewebe oder Substanzen in regelmäßigen Abständen erneuert werden müssen. Der Plan zur Herstellung eben genannter Strukturen ist in der DNS kodiert.
- Definition
- Die $\textbf{DNS}$ ist ein zweistrangiges Molekül, welches Nukleotiden und Wasserstoffbrücken besteht.
Die Abfolge der Nukleotide, genauer der Basenteil des Nukleotid, kodieren die Aminosäuren.
Evolutionäre Algorithmen
Pseudo-code
Merke
Die evolutionären Algorithmen haben sich ursprünglich an der natürlichen Evolution orientiert, wie auch bei den technischen Prozessen ist es jetzt jedoch ein sehr spezielles Teilgebiet der Informatik was wenig mit den Ursprüngen verbindet. Die Fortschritte die auf diesem Gebiet erzielt wurden wandern, erstaunlicher weise wieder zurück zu ihren Wurzeln und bieten der Biologie ein Sammelsurium an Werkzeugen die diesem Gebiet zu neuen Erkenntnissen verhelfen.
Quellen
- Wagenknecht, 2003, Algorithmen und Komplexität
- von Rimscha, 2008, Algorithmen kompakt und verständlich
- Wanka, 2006, Approximationsalgorithmen
- Heun, 2000, Grundlegende Algorithmen
- Cormen/Leiserson/Rivest/Stein, 2007, Algorithmen - Eine Einführung
- Vorlesung Simulation natürlicher Vorgänge, Westfälische Wilhelms-Universität Münster (Folien 4 -- 16, Kapitel 8)