Prioritätswarteschlangen WS13-14
Aus ProgrammingWiki

Inhaltsverzeichnis
|
Warteschlange
Benutzen das "First in, First out" Prinzip. Es kann eine beliebige Menge von Objekten aufnehmen und gibt diese in der Reihenfolge ihres Einfügens wieder zurück
Beispiele für Warteschlangen sind Autos an einer Zapfsäule, Warteschlange im Supermarkt, Patienten im Wartezimmer, Prozesse in einem Computerbetriebssystem.
Methoden
-1. enqueue - neue elemente in einer liste einfügen
-2. dequeue - entfernt das erste element in einer liste
Amortisierte Laufzeitanalyse
dient zur ermittlung der mittleren Laufzeit einer operation in einer folge von operationen. Allerdings wird nicht mehr Laufzeit einzelner Operationen analysiert, sondern die Gesamtlaufzeit einer Folge von Operationen. Erhalten dann, wie viel Zeit im Durchschnitt jede Operation der Folge benötigt.
Methoden
-1. Amortisierte Analyse durch Zusammenfassung - die durchschnittlichen Kosten einer Einzeloperation zu ermitteln, indem man zunächst die Gesamtkosten aller Operationen ermittelt und diese dann durch die Anzahl der Operationen dividiert.
-2. Buchhaltungsmethode - ermittlung der Laufzeit für jede Operation. Die ermittelten Werte können größer sein als eigentliche Laufzeiten einer Operation. Diesen Überschuss können wir nutzen für Operationen, deren werte kleiner sind als ihre eigentliche Laufzeit. Dabei ist zu beachten, dass die Gesamtlaufzeit niemals negativ sein darf.
-3. Potentialmethode - zuordnung von Laufzeiten zu verschiedenen operationen. Die Differenz zwischen der amortisierten und der eigentlichen Laufzeit wird als Ganzes in Form eines Potenzials zur Verfügung gestellt.
Prioritätswarteschlangen
Prioritätswarteschlange - Definition und Beispiel
- Eine Prioritätswarteschlange (auch: Vorrangwarteschlange, Prioritätenliste, Prioritätsschlange) ist eine specielle Art der abstrakte Datenstruktur. Das ist die Erweiterung der Warteschlange. Die Werte bekommen einmalige Schlüssel (jede Schlüssel hat nur ein Wert!) und sie sind in Reihenfolge mit der bestimmte Ordnung. Am meisten der Prioritätswarteschlangen können wir mit Assoziatives Datenfeld oder Heap realizieren.
Wir können ganz einfach sagen, dass: Prioritätswarteschlange ist die abstrakte Datenstruktur, die die Elemente von Menge S deponieren. Diese Elemente haben bestimmte Werte, welche wir können "Schlüssel" heißen und sie sind bis andere Werte in eine Ordnung zusammenpassen.
Wann nutzen wir von Prioritätswarteschlange?
-Dijkstra-Algorithmus
-Algorithmus von Prim
-Huffman-Kodierung
-Heapsort
Beispiel
Person in Pseudocode
Prioritätswarteschlange - Operationen
In Prioritätswarteschlange können wir von verschiedene Operationen nutzen. Manchmal (verschidene Quellen) haben andere Namen (z.B. FindMin und Minimum). Operationen sind sehr nützlich in verschiedene Sprachenprogramme, mehr hier. Sie sind am meistens als API in diese Sprachen implementiert, genauer als Bibliotheken in diese Fall.
MakePQ()
- bilden neu leer Schlange
- Es gibt keine Wurzel und Blätter.
Insert(H,x)
- hinzufügen bis Schlange H ein neu Element x
- Wenn in Schlange schon andere Element sind, dass diese neu immer Blatt ist
- Wenn Schlange leer ist, ist neu Element in diese Fall als Wurzel.
Delete(H,x)
- löscht Element x von Schlange H
- in diese "leer" Plätze geben wir die Element, die auf die letzte Plätze ist.
- Sortierung mit bestimmte Ordnung
FindMin(H)
- sucht Element von Schlange H mit am kleinste Schlüssel
- zurückgeben diese Element
DelMin(H)
- sucht Element von Schlange H mit am kleinste Schlüssel
- löscht diese Element von Schlange H
DecreaseKey(H,x,y)
- in Schlange H, für bestimmte Element x, gibt neue, kleinere Werte y
- Sortierung mit bestimmte Ordnung, weil neue Werte nicht in gute Plätze sein kann
Prioritätswarteschlangen - Laufzeit
| Operation | Binärer Heap | Binomial Heap | Fibonacci Heap |
|---|---|---|---|
| MakePQ | | | |
| FindMin | | | |
| Delete | | | |
| Insert | | | |
| DecreaseKey | | | |
| DelMin | | | |
| Meld | | | |
Assoziatives Datenfeld
Das assoziative Datenfeld (englisch „map“, „dictionary“ oder „associative array“) ist eine Art der abstrakte Datenstruktur. Diese Struktur deponiert die Paare Daten(Schlüssel, Wert), die der Wert und der einmalig Schlüssel haben. Mithilfe bestimmte Schlüssel haben wir der Zutritt bis genau ein Wert.
API den vielen Programmiersprachen nutzen von Assoziatives Datenfeld, z.B.: Java, C++, C#, PHP, Python, Ruby, LISP, D, JavaScript.
Beispiel in C++
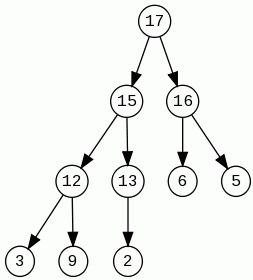
Binäre Heap
Heap ist die speziell Zufall der Binäre Baum, wo jede "Kind" ist nicht größer als seine "Eltern". Aufgrund diese Bedingungen wir sagen können, dass:
-Wurzel muss am größsten sein, oder mit andere am größte Wert haben,
-auf Verknüpfungen(von Wurzel bis Blätter) Werte können nicht steigen.
Voll Heap ist, wenn auf alle Niveau (ohne letzte) voll sind und auf letzte Nivou sind den chronologisch Blätter ordnen.
Prioritätswarteschlangen auf Heap
Auf Heap können wir Prioritätswarteschlangen (auch bestimmte operationen) nutzen.
Wir können neue Elemente hinzufügen und bekommen zurück immer am größsten.
Insert
Mithilfe Insert können wir in erste freie Plätze das latzte Niveau hinzufügen und dann, wenn neue Element größer als seine Elternteil ist, können wir einander tauschen. Jetzt müssen wir überprüfen mit nächste Element in Hierarchie, und mit nächste... bis Wurzel.
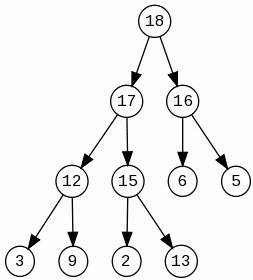
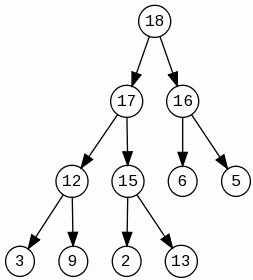
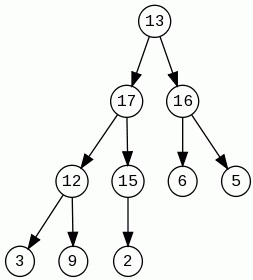
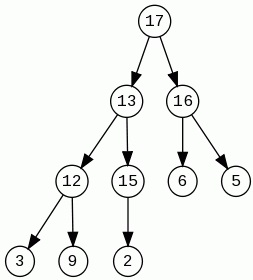
Delete Max
Diese Operation löscht am gröbste Element (Wurzel) in unsere Baum. In neue leere Plätze geben wir die letzte (erst von recht Seite) Element auf unterste Niveau. Jetzt überprüfen wir mit "größere Kind" und wenn diese Kind größer ist, tauschen wir Plätzen diese 2 Elemente. Das machen wir so lang, wenn es keine größere Kinder gibt, oder diese Element ist Blatt.
Binominal Heaps
Binominal Heaps ist sehr ähnlich wie normale Heaps. Das ist auch die abstrakte Datenstruktur. Welche sind Unterschiede zwischen ganz normale Heaps und binomal Heaps?
Binominal Heaps nutzen auch von Operationen wie Insert, FindMin, usw... aber hat auch Meld(H1,H2). Was macht das?
- Meld(H1,H2)
- Verbindung zwei Schlangen, H1 mit H2
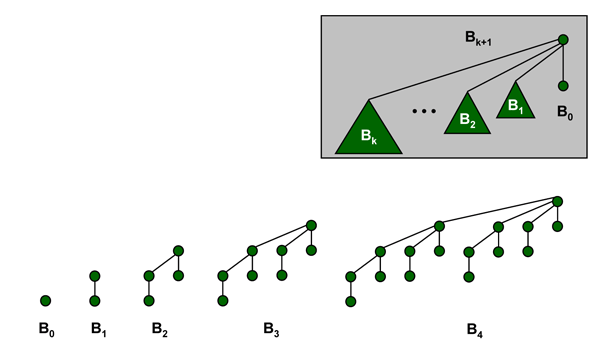
Diese Datenstruktur hat specielle Eigenschaften, die Binominal Heap $B_{k}$:
- hat $2^{k}$ Elemente
- Höhe ist k
- funktioniert $0 \le i \le k$ ($i$ ist Niveau)
Fibonacci Heaps
Fibonacci Heaps ist auch Datenstruktur. Diese Heaps ist sehr ähnlich wie Binominal Heaps aber ist seine Verbesserung, die mit ständig amortisierte Kosten DecreaseKey (z.B. in Dijkstry Algorithmus ist). Die Grundidee ist sehr einfach, sie macht manches Operationen später, bis Moment, wenn wirklich notwendig ist. Gleich wie Binominal Heaps, Fibonacci Heaps ist auch die Liste den Bäumen, von welche jede ist in bestimmte Ordnung Heaps.
Dijkstra-Algorithmus
Wie sollen wir diese Name sprechen?
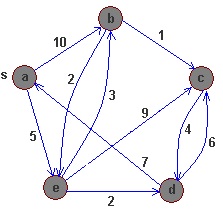
Dijkstra-Algorithmus nutzen wir bis Suche am kürzte Abstand von bestimmte Eckpunkt s bis alle andere Eckpunkte. In diese Algoritmus, Graph-Eingang kann nicht Kante mit Zahlen < 0 haben. Kanten haben aber Vektoren. Grundaufgabe ist Suche alle Q Eckpunkte in Menge, für welche gibt es noch keine am kurzte Wege (am Anfang stehen hier immer alle Eckpunkte) und Vektor von s bis alle Eckpunkte i.
Wie funktioniert diese Algorithmus?
1) Solange Menge Q ist nicht leer, macht
2) Nehmen von Menge Q der Eckpunkt v, welche am kleinste Wert hat
3) Für jede nächste Eckpunkt v, überpruft ob er mit vorige Eckpunkt (d.h. Summe den Werte) ist kleiner als andere diese Verbindungen oder einzeln Weg.
| (a) | (b) | (c) | (d) | (e) | |
| (a) | 0 | 10 | $\infty$ | $\infty$ | 5 |
| (b) | $\infty$ | 0 | 1 | $\infty$ | 2 |
| (c) | $\infty$ | $\infty$ | 0 | 4 | $\infty$ |
| (d) | 7 | $\infty$ | 6 | 0 | $\infty$ |
| (e) | $\infty$ | 3 | 9 | 2 | 0 |
| Q | (a) | (b) | (c) | (d) | (e) |
| {b,c,d,e} | 0 | 10 | * | * | 5 |
| {b,c,d} | 0 | 8 | 14 | 7 | 5 |
| {b,c} | 0 | 8 | 13 | 7 | 5 |
| {c} | 0 | 8 | 9 | 7 | 5 |
| {} | 0 | 8 | 9 | 7 | 5 |
Übungen
Teil 1
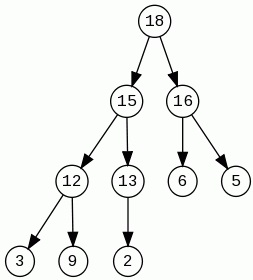
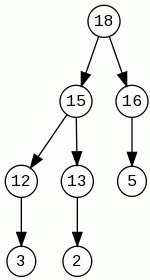
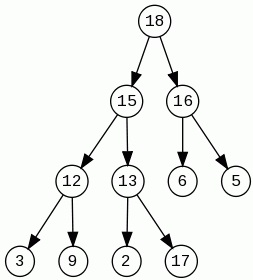
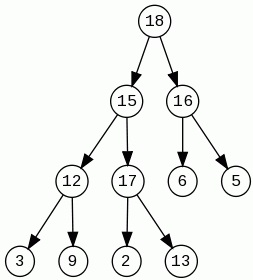
1. Skizzieren Sie den Heap, der sich ergibt, wenn die folgenden Operationen mit einem ursprünglich leeren Heap ausgeführt werden: Insert(10), Insert(5), Insert(6), Insert(8), Remove(6), Insert(7), Insert(3), Insert (2), DelMin.
2. Ist eine Datei in umgekehrt sortierter Reihenfolge ein Heap?
Teil 2
 | S3makrza_Übungen.pdf (0.6 MB) |
Literatur
- http://www.algorytm.org/
- http://wazniak.mimuw.edu.pl
- http://iair.mchtr.pw.edu.pl/
- http://pl.wikipedia.org/wiki/Wikipedia:Strona_g%C5%82%C3%B3wna
- http://de.wikipedia.org/wiki/Wikipedia:Hauptseite