Hilfsmittel Mathematik 1 SS09
Aus ProgrammingWiki
Inhaltsverzeichnis |
Autoren
Igor Geiger ,Ralf Bergmann
Exponentialfunktionen und Lineare Regression
Bei der Analyse von Algorithmen zur Bestimmung des Aufwandes ,für eine bestimmte Anzahl an Eingabegrößen,die von der Anwendung des Algorithmus abhängt,tritt eine Punktmenge im Kartesischen Koordinatesystem auf,die exponentiel beschrieben werden kann. In realen Meßungen ergibt sich aber meistens eine verworfene Punktmenge die einer Exponentialfunktion angenährt werden kann.Jedoch lässt sich anhand dieser Kurve der Aufwand des Algorithmus nicht exakt bestimmen da man dazu einen exakten Anstieg braucht bzw. eine exakte Funktion. Dazu würd die entstandene Punktmenge in ein Kartesiches Koordinatensystem mit einer logarithmischen y-Achse überführt.
Darstellung von im neuen System nach Gnuplot.
Es entsteht folgende Gerade,Schnittpunkt bei y=10 mit der y-Achse:
Darstellung von im logarithmischen System:
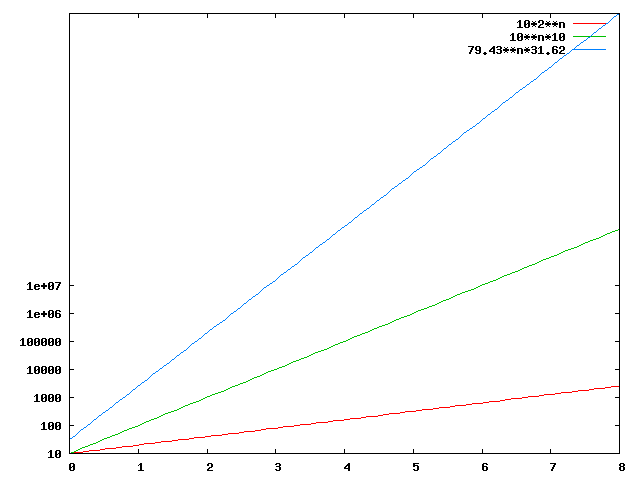
Dies entspricht,vom Aussehen,der Geraden im normalen kartesischen Koordinatensystem:
Desweiteren hat sich gezeigt das es viel einfacher ist eine Gerade im dargestellten Logarithmischen Koordinatensystem anhand der eingetragenen Punkte zu verlegen als eine Exponentialfunktion im normalen Koordinatensystem zu bestimmen.
Die mathematische Methode zur Bestimmung einer Geraden im logarithmischen Koordinatensystem,anhand der verstreuten Messpunkte,nennt man Lineare Regression.
Die Gerade soll so bestimmt werden das der maximale Abstand zwischen der Geraden und den Messpunkten möglichst klein wird.
Mathematische Vorgehensweise:
Da es für jeden Messpunkt gelten muß,würd die gesuchte Funktion als Summe der Abstände der einzelnen Messpunkte dargestellt:
Von der entstandenen Funktion wird aber zur Bestimmung des Minimums die erste Ableitung benötigt
jedoch ist die Betragsfunktion an der Stelle nicht stetig differenzierbar.
Dazu Quadriert man sie nach der Methode der kleinsten Fehlerquadrate von Gauss,dadurch wird sie
Differenzierbar aber die Suche nach dem Minimum wird dadurch nicht beeinflußt.
Für das Minimum muß die erste Ableitung der obigen Funktion Null gesetzt werden.
Da man aber das Minimum nach a und b haben will muß man auch jeweils nach a und b ableiten.
Ableitung nach a:
Ableitung nach b:
Durch Vereinfachung erhält man die sogennante Normalengleichung:
Durch weiteres Umstellen nach a bzw. b erhält man die gewünschten Parameter für die Regressionsgerade.
Umformung nach a:
Somit erhält man die Parameter a und b für die Regressionsgerade:
Beispielrechnung:
folgende Meßwerte:
T(1)=3
T(2)=6
T(3)=7
T(4)=9
T(5)=11
In die Gleichung für a und b einsetzen!
Parameter für die Regressionsgerade im kartesischen Koordinatensystem.
Würde man die folgenden Messpunkte im logarithmischen Koordinatensystem als ansteigende Gerade erkennen so wäre die Gleichung zur Exponentialfunktion dieser Geraden
Wobei dan aber gelten muß : (das a von der Regressionsgeraden oben)
dabei ergibt sich für unser Beispiel folgende Exponentialfunktion:

Polynomfunktion
Ein Graph wird zur Gerade wenn beide Achsen logarithmisch eingestellt sind.
Bei Funtionen folgender Gestalt:
Diese Funtion kann weiter beschrieben werden als:
Daraus ergibt sich folgender Funktionsgraph mit normaler Achseneinteilung für:
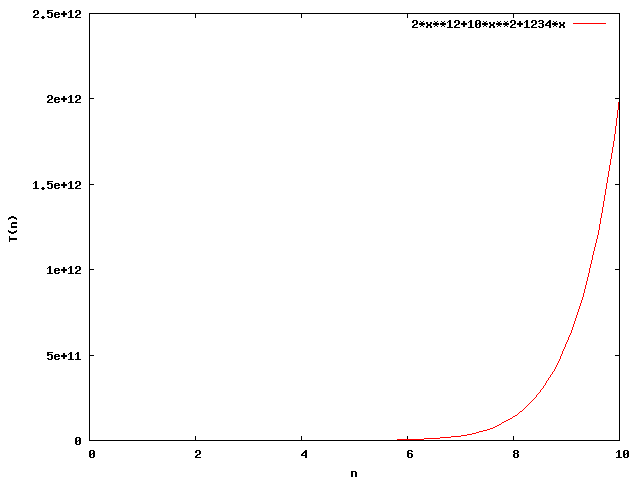
Dieser Graph ist keine Gerade, deshalb müssen wir die logarithmische Achseneinteilung wählen um auf das gewünschte Ergebnis zu kommen.
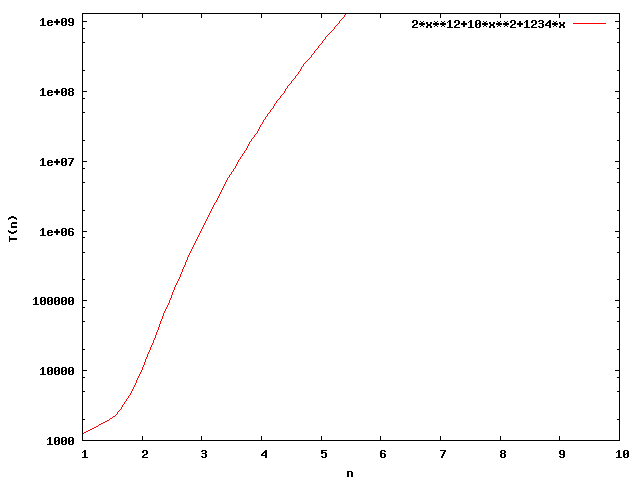
Funktionsgraph mit logarithmischer y-Achseneinteilung:
Funktionsgraph mit logarithmischer x- und y-Achseneinteilung:
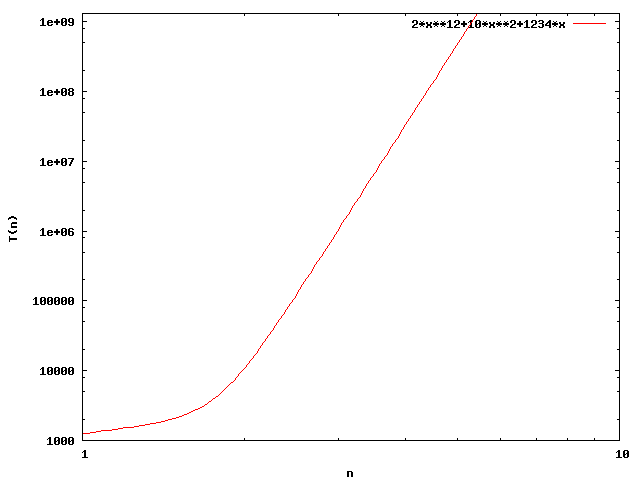
Bei diesen Graphen handelt es sich um keine Gerade weil eine Summe gebildet wird.
Schließlich kann man davon ausgehen das nicht bei jeder Funktion eine Gerade ensteht.
Deshalb sind andere Untersuchungsmethoden notwendig um auf das gewünschte Ergebnis zu kommen.
Polynomfunktionen bestehen aus mehreren Basisfunktionen der folgenden Form:
Die Lösung des Problems ergibt sich durch Anwenden der Methode der kleinsten
Fehlerquadrate auf die Polynomfunktion.
Die Methode der kleinsten Fehlerquadrate angewandt auf die Formel:
Das heißt die Summe der Abstände (n Messpaare, also n Abstände) zwischen der gesuchten Funktion und den Messwerten soll minimal werden. Dazu bildet man die Ableitung und setzt diese Null.
Dazu multipliziert man die Ableitung aus und bringt auf die rechte Seite.
Dabei ist eine der Basisfunktionen zwischen 0 und m. Um eine Lösung für
alle c zu erhalten, trägt man die Formeln in ein lineares Gleichungssystem
ein. Um dieses dann zu lösen, werden für
alle Basisfunktionen angenommen.
Um das besser repräsentieren zu können, wählt man eine Darstellung
mit Hilfe von Matrizen
Der Faktor ist die Transpornierte der Matrix A. Daraus ergibt sich die
Form
Damit kann man dieses Gleichungssystem nach lösen und erhält die Faktoren
für die einzelnen Polynome.
Maple-Worksheet (Maple 11)
restart:
with(linalg):
with(plots):
x := [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
y := [0, 4, 9, 16, 25, 36, 49, 64, 81, 100];
g := x->x^0, x->x, x->x^2, x->x^3;
n := nops(x);
m := nops([g])-1;
A := matrix(n, m+1, 0):
c := vector(m, 0):
for k to n do
for i to m+1 do
A[k, i] := g[i](x[k]);
od:
od:
evalm(A);
AT := transpose(A):
left := evalm(AT&*A):
right := (AT&*y):
c := evalf(linsolve(left, right));
x:=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
y:=[0, 4, 9, 16, 25, 36, 49, 64, 81, 100]
2 3
g:=x -> 1, x -> x, x -> x , x -> x
n:=10
m:=3
c:=[0.1762237762,2.635198135,0.8671328671,0.008158508158]
h := 0: for i from 0+1 to m+1 do h := h+c[i]*g[i] od: pkt := [seq([x[i], y[i]], i = 1 .. n)]: bild1 := plot(pkt, 0 .. x[n], 0 .. y[n], style = point, symbol = diamond); bild2 := plot(h(xx), xx = x[1] .. x[n], color = BLACK); display(bild1, bild2, labels = ['x', 'h(x)']);
Übungsaufgaben
Folien
- Hier sind die Folien zur Vorlesung
 | Hilfsmittel_Mathematik1_v1.pdf (0.8 MB) |